Reference:

• Hilderman, R.J. and Hamilton, H.J., ``Evaluation of Interestingness Measures for Ranking Discovered Knowledge,'' In Pacific-Asia Conference on Knowledge Discovery and Data Mining (PAKDD-01), Hong Kong, Springer Verlag, April, 2001, pp. 247-259.
• Hilderman, R.J., and Hamilton, H.J. ``Measuring the Interestingness of Discovered Knowledge: A Principled Approach,'' Intelligent Data Analysis, 7(4):347-382, 2003.

Introduction

An important problem in the area of data mining is the development of effective measures interestingness for ranking discovered knowledge. The five principles that we will refer to as the the Measure of Interestingness Principles provide a foundation for an intuitive understanding of the term "interestingess" when used within this context.

We examine functions f of m variable, f(n₁,...,n_n) where f denotes a general mesaure of diversity, m and each n_i ( n_i assumed to be non-zero), are as defined in the previous section, and f(n₁,...,n_n is a vector corresponding to the values in the derived Count attribute (or numeric measure attribute) for some arbitrary summary whose values are arranged in descending order such that n₁ >= ... >= n_m (except for discussions regarding I_Lorenz, which requires that the values be arranged in ascending order). Since the principles presented here are for ranking the interestingess of summaries generated from a single dataset, we assume that N is fixed.

P1 - Minimum Value Principle

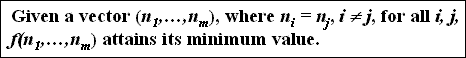
• Minimum interestingness should be attained when the tuple counts are equal. (i.e., uniformly distributed).
• given the vectors (2,2), (50,50,50), and (1000,1000,1000,1000), we require that f(2,2) = f(50,50,50) = f(1000,1000,1000,1000) and the the index value generated by f be the minimum possible

P2 - Maximum Value Principle

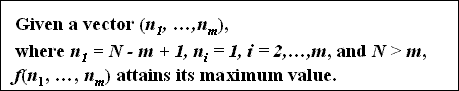
• Maximum interestingness should be attained when the tuple counts are distributed as unevenly as possible.
• given the vectors (3,1), (148,1,1) and (3997,1,1,1), where m = 2,3, and 5, respectively and N= 4, 150, and 4000, respectively, we require that the index value generated by f be the maximum possible for the respective values for m and N

P3 - Skewness Principle

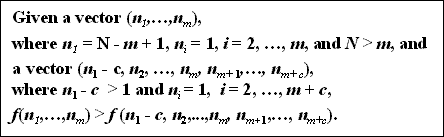
• a summary containing m tuples whose counts are distributed as unevenly as possible will be more interesting than a summary containing m + c tuples, whose counts are also distributed as unevenly as possible.
• for example, with N = 1000, m = 2, c = 2, the vectors are (999,1) and (997,1,1,1) and we require that f(999,1) > f(997,1,1,1).

P4 - Permutation Invariance Principle

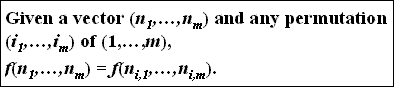
• Every permutation of a given distribution of tuple counts should be equally interesting.
• Interestingness is not labeled property, it can be only determined by the distribution of the counts
• Given the vector (6,4,2), we require that f(6,4,2) = f(2,4,6) = f(4,2,6) =f(4,6,2) = f(2,6,4) = f(6,2,4).

P5 - Transfer Principle

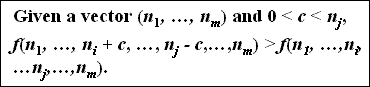
• When a strictly positive transfer is made from the count of one tuple to another tuple whose count is greater, then interestingness increases.
• For example, given the vectors (10,7,5,4) and (10,9,5,2), we require that f(10,9,5,2) > f(10,7,5,4).

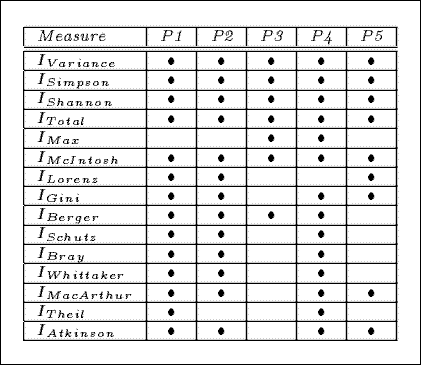
Measures Satisfying the 5 Principles

The following table identifies the measures that satisy the principles of interestingness. In the table the P1 to P5 columns describe the principles, and a measure that satisfies a principle in denoted by the bullet symbol