Overview of Decision Trees

References:

• T. Mitchell, "Decision Tree Learning", in T. Mitchell, Machine Learning, The McGraw-Hill Companies, Inc., 1997, pp. 52-78.
• P. Winston, "Learning by Building Identification Trees", in P. Winston, Artificial Intelligence, Addison-Wesley Publishing Company, 1992, pp. 423-442.

Decision tree learning is a method that uses inductive inference to approximate a target function, which will produce discrete values. It is widely used, robust to noisy data, and considered a practical method for learning disjunctive expressions.

Appropriate Problems for Decision Tree Learning

Decision tree learning is generally best suited to problems with the following characteristics:

• Instances are represented by attribute-value pairs.
  • There is a finite list of attributes (e.g. hair colour) and each instance stores a value for that attribute (e.g. blonde).
  • When each attribute has a small number of distinct values (e.g. blonde, brown, red) it is easier for the decision tree to reach a useful solution.
  • The algorithm can be extended to handle real-valued attributes (e.g. a floating point temperature)
• The target function has discrete output values.
  • A decision tree classifies each example as one of the output values.
    • Simplest case exists when there are only two possible classes (Boolean classification).
    • However, it is easy to extend the decision tree to produce a target function with more than two possible output values.
  • Although it is less common, the algorithm can also be extended to produce a target function with real-valued outputs.
• Disjunctive descriptions may be required.
  • Decision trees naturally represent disjunctive expressions.
• The training data may contain errors.
  • Errors in the classification of examples, or in the attribute values describing those examples are handled well by decision trees, making them a robust learning method.
• The training data may contain missing attribute values.
  • Decision tree methods can be used even when some training examples have unknown values (e.g., humidity is known for only a fraction of the examples).

After a decision tree learns classification rules, it can also be re-represented as a set of if-then rules in order to improve readability.

Decision Tree Representation

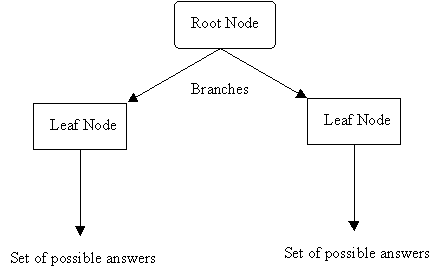
A decision tree is an arrangement of tests that provides an appropriate classification at every step in an analysis.

"In general, decision trees represent a disjunction of conjunctions of constraints on the attribute-values of instances. Each path from the tree root to a leaf corresponds to a conjunction of attribute tests, and the tree itself to a disjunction of these conjunctions" (Mitchell, 1997, p.53).

More specifically, decision trees classify instances by sorting them down the tree from the root node to some leaf node, which provides the classification of the instance. Each node in the tree specifies a test of some attribute of the instance, and each branch descending from that node corresponds to one of the possible values for this attribute.

An instance is classified by starting at the root node of the decision tree, testing the attribute specified by this node, then moving down the tree branch corresponding to the value of the attribute. This process is then repeated at the node on this branch and so on until a leaf node is reached.

Diagram

• Each nonleaf node is connected to a test that splits its set of possible answers into subsets corresponding to different test results.
• Each branch carries a particular test result's subset to another node.
• Each node is connected to a set of possible answers.

Occam's Razor (Specialized to Decision Trees)

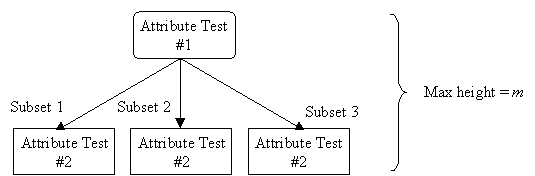
Given m attributes, a decision tree may have a maximum height of m.

Rather than building all the possible trees, measuring the size of each, and choosing the smallest tree that best fits the data, we use Quinlan's ID3 algorithm for constructing a decision tree.