Dynamic Itemset Counting

References:
S. Brin, R. Motwani, J.D. Ullman, S. Tsur, "Dynamic Itemset Counting and Implication Rules for Market Basket Data", SIGMOD Record, Volume 6, Number 2: New York, June 1997, pp. 255 - 264.

Su, Yibin, Dynamic Itemset Counting and Implication Rules for Market Basket Data: Project Final Report, CS831, April 2000.

Introduction

Alternative to Apriori Itemset Generation
Itemsets are dynamically added and deleted as transactions are read
Relies on the fact that for an itemset to be frequent, all of its subsets must also be frequent, so we only examine those itemsets whose subsets are all frequent

Algorithm stops after every M transactions to add more itemsets.

Train analogy: There are stations every M transactions. The passengers are itemsets. Itemsets can get on at any stop as long as they get off at the same stop in the next pass around the database. Only itemsets on the train are counted when they occur in transactions. At the very beginning we can start counting 1-itemsets, at the first station we can start counting some of the 2-itemsets. At the second station we can start counting 3-itemsets as well as any more 2-itemsets that can be counted and so on.

Itemsets are marked in four different ways as they are counted:

Solid box: confirmed frequent itemset - an itemset we have finished counting and exceeds the support threshold minsupp
Solid circle: confirmed infrequent itemset - we have finished counting and it is below minsupp
Dashed box: suspected frequent itemset - an itemset we are still counting that exceeds minsupp
Dashed circle: suspected infrequent itemset - an itemset we are still counting that is below minsupp

DIC Algorithm

Algorithm:

Mark the empty itemset with a solid square. Mark all the 1-itemsets with dashed circles. Leave all other itemsets unmarked.
While any dashed itemsets remain:
1. Read M transactions (if we reach the end of the transaction file, continue from the beginning). For each transaction, increment the respective counters for the itemsets that appear in the transaction and are marked with dashes.
2. If a dashed circle's count exceeds minsupp, turn it into a dashed square. If any immediate superset of it has all of its subsets as solid or dashed squares, add a new counter for it and make it a dashed circle.
3. Once a dashed itemset has been counted through all the transactions, make it solid and stop counting it.

Itemset lattices: An itemset lattice contains all of the possible itemsets for a transaction database. Each itemset in the lattice points to all of its supersets. When represented graphically, a itemset lattice can help us to understand the concepts behind the DIC algorithm.

Example: minsupp = 25% and M = 2.

TID	A	B	C
T1	1	1	0
T2	1	0	0
T3	0	1	1
T4	0	0	0

Transaction Database

Itemset lattice for the above transaction database:
Itemset lattice before any transactions are read:
Counters: A = 0, B = 0, C = 0
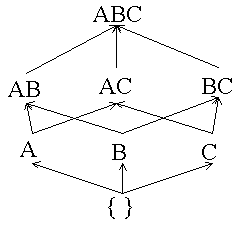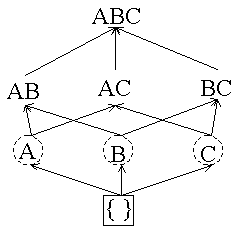Empty itemset is marked with a solid box. All 1-itemsets are marked with dashed circles.

After M transactions are read: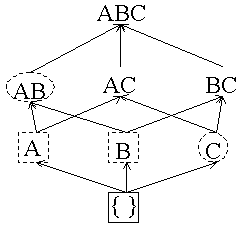

Counters: A = 2, B = 1, C = 0, AB = 0
We change A and B to dashed boxes because their counters are greater than minsup (1) and add a counter for AB because both of its subsets are boxes.
After 2M transactions are read: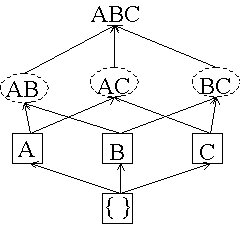
Counters: A = 2, B = 2, C = 1, AB = 0, AC = 0, BC = 0
C changes to a square because its counter is greater than minsup.A, B and C have been counted all the way through so we stop counting them and make their boxes solid. Add counters for AC and BC because their subsets are all boxes.

After 3M transactions read: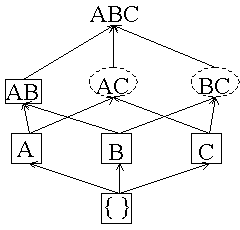
Counters: A = 2, B = 2, C = 1, AB = 1, AC = 0, BC = 0
AB has been counted all the way through and its counter satisfies minsup so we change it to a solid box. BC changes to a dashed box.

After 4M transactions read: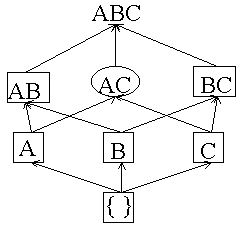
Counters: A = 2, B = 2, C = 1, AB = 1, AC = 0, BC = 1
AC and BC are counted all the way through. We do not count ABC because one of its subsets is a circle. There are no dashed itemsets left so the algorithm is done.

Implementation

Go to the DIC Implementation page to see a working implementation in Java.

Operations:

add new itemsets
maintain a counter for every itemset
manage itemset states from dashed to solid and from circle to square
when itemsets become large determine which new itemsets should be added because they could potentially be large

Pseudocode Algorithm:

SS = Æ ;    // solid square (frequent)
SC = Æ ;   // solid circle (infrequent)
DS = Æ ;   // dashed square (suspected frequent)
DC = { all 1-itemsets } ;   // dashed circle (suspected infrequent)
while (DS != 0) or (DC != 0) do begin
    read M transactions from database into T
    forall transactions t ÎT do begin
        //increment the respective counters of the itemsets marked with dash
        for each itemset c in DS or DC do begin
            if ( c Î t ) then
                c.counter++ ;
        for each itemset c in DC
            if ( c.counter ³ threshold ) then
                move c from DC to DS ;
                if ( any immediate superset sc of c has all of its subsets in SS or DS ) then
                    add a new itemset sc in DC ;
        end
        for each itemset c in DS
            if ( c has been counted through all transactions ) then
                move it into SS ;
        for each itemset c in DC
            if ( c has been counted through all transactions ) then
                move it into SC ;
    end
end

Answer = { c Î SS } ;

Itemset lattice for the above transaction database:	Itemset lattice before any transactions are read: Counters: A = 0, B = 0, C = 0 Empty itemset is marked with a solid box. All 1-itemsets are marked with dashed circles.
After M transactions are read: Counters: A = 2, B = 1, C = 0, AB = 0 We change A and B to dashed boxes because their counters are greater than minsup (1) and add a counter for AB because both of its subsets are boxes.	After 2M transactions are read: Counters: A = 2, B = 2, C = 1, AB = 0, AC = 0, BC = 0 C changes to a square because its counter is greater than minsup.A, B and C have been counted all the way through so we stop counting them and make their boxes solid. Add counters for AC and BC because their subsets are all boxes.
After 3M transactions read: Counters: A = 2, B = 2, C = 1, AB = 1, AC = 0, BC = 0 AB has been counted all the way through and its counter satisfies minsup so we change it to a solid box. BC changes to a dashed box.	After 4M transactions read: Counters: A = 2, B = 2, C = 1, AB = 1, AC = 0, BC = 1 AC and BC are counted all the way through. We do not count ABC because one of its subsets is a circle. There are no dashed itemsets left so the algorithm is done.