


 |
Inductive Inference |   |
Reference: T. Mitchell, 1997.
Inductive inference is the process of reaching a general conclusion from specific examples.
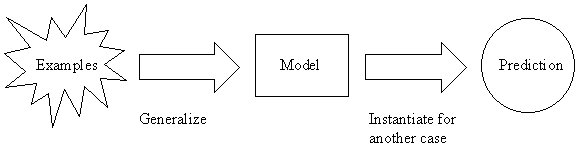
The general conclusion should apply to unseen examples.
Inductive Learning Hypothesis: any hypothesis found to approximate the target function well over a sufficiently large set of training examples will also approximate the target function well over other unobserved examples.
Example:
Identified relevant attributes: x, y, z
| x | y | z |
| 2 | 3 | 5 |
| 4 | 6 | 10 |
| 5 | 2 | 7 |
Model 1:
x + y = z
Prediction: x = 0, z = 0 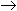 y = 0
y = 0
Model 2:
if x = 2 and z = 5, then y = 3.
if x = 4 and z = 10, then y = 6.
if x = 5 and z = 7, then y = 2.
otherwise y = 1.
Model 2 is likely overfitting.
| Good: | completely consistent with data. |
| Bad: | no justification in the data for the prediction that y = 1 in all other cases. |
| not in the class of algebraic functions (but nothing was said about class of descriptions). |
Inductive bias: explicit or implicit assumption(s) about what kind of model is wanted.
Typical inductive bias:
Example:
Some languages of interest:
Positive and Negative Examples
Positive Examples
| x | y | z |
| 2 | 3 | 5 |
| 2 | 5 | 7 |
| 4 | 6 | 10 |
| general | x, y, z  I I |
| more specific | x, y, z  I+ I+ |
| more specific than the first two | 1 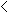 x, y, z x, y, z 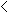 11 ; x, y, z 11 ; x, y, z 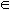 I I |
| even more specific model | x + y = z |
Negative Examples
| x | y | z | Decision |
| 2 | 3 | 5 | Y |
| 2 | 5 | 7 | Y |
| 4 | 6 | 10 | Y |
| 2 | 2 | 5 | N |
Search for Description
Description keeps getting larger or longer.
Finite language - algorithm terminates.
Infinite language - algorithm runs
X = example space/instance space (all possible examples)
D = description space (set of descriptions defined as a language L)
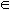 L
corresponds to a set of examples Xl.
L
corresponds to a set of examples Xl.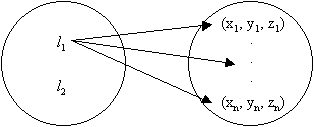
Success Criterion
Look for a description l 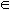 L such that l is consistent with all observed examples.
L such that l is consistent with all observed examples.
Example:
L = {x op y = z}, op = {+, -, *, /}
Given a precise specification of language and data, write a program to test descriptions one by one against the examples.
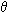 (|L| * |X|)
(|L| * |X|)Why is Machine Learning Hard (Slow)?
It is very difficult to specify a small finite language that contains a description of the examples.
e.g., algebraic expressions on 3 variables is an infinite language
 |
  |