


 |
Overview of Decision Trees |   |
References:
Robust to noisy data and capable of learning disjunctive expressions, decision tree learning, a method for approximating discrete-valued target functions, is one of the most widely used and practical methods for inductive inference.
Appropriate Problems for Decision Tree Learning
Decision tree learning is generally best suited to problems with the following characteristics:
Learned functions are either represented by a decision tree or re-represented as sets of if-then rules to improve readability.
Decision Tree Representation
A decision tree is an arrangement of tests that prescribes an appropriate test at every step in an analysis.
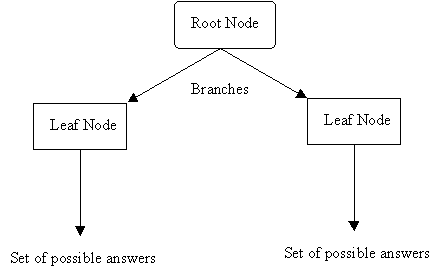
In general, decision trees represent a disjunction of conjunctions of constraints on the attribute-values of instances. Each path from the tree root to a leaf corresponds to a conjunction of attribute tests, and the tree itself to a disjunction of these conjunctions.
More specifically, decision trees classify instances by sorting them down the tree from the root node to some leaf node, which provides the classification of the instance. Each node in the tree specifies a test of some attribute of the instance, and each branch descending from that node corresponds to one of the possible values for this attribute.
An instance is classified by starting at the root node of the decision tree, testing the attribute specified by this node, then moving down the tree branch corresponding to the value of the attribute. This process is then repeated at the node on this branch and so on untila leaf node is reached.
Diagram
Occam's Razor (Specialized to Decision Trees)
"The world is inherently simple. Therefore the smallest decision tree that is consistent with the samples is the one that is most likely to identify unknown objects correctly."
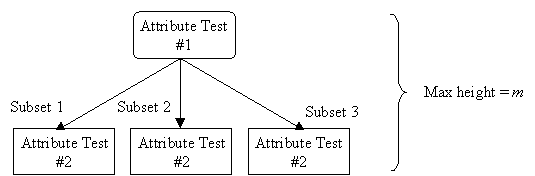
Given m attributes, a decision tree may have a maximum height of m.
Rather than building all the possible trees, measuring the size of each, and choosing the smallest tree that best fits the data, we use Quinlan's ID3 algorithm for constructing a decision tree.
 |
  |