


 |
Decision Tree Rules & Pruning |   |
References:
Rule Generation
Once a decision tree has been constructed, it is a simple matter to convert it into an equivalent set of rules.
Converting a decision tree to rules before pruning has three main advantages:
To generate rules, trace each path in the decision tree, from root node to leaf node, recording the test outcomes as antecedents and the leaf-node classification as the consequent.
Rule Simplification Overview
Once a rule set has been devised:
The following is a contingency table, a tabular representation of a rule.
| C1 | C2 | Marginal Sums | |
| R1 | x11 | x12 | R1T = x11 + x12 |
| R2 | x21 | x22 | R2T = x21 + x22 |
| Marginal Sums | CT1 = x11 + x21 | CT2 = x12 + x22 | T = x11 + x12 + x21 + x22 |
R1 and R2 represent the Boolean states of an antecedent for the conclusions C1 and C2
(C2 is the negation of C1).
x11, x12, x21 and x22 represent the frequencies of each antecedent-consequent pair.
R1T, R2T, CT1, CT2 are the marginal sums of the rows and columns, respectively.
The marginal sums and T, the total frequency of the table, are used to calculate expected cell values in step 3 of the test for independence.
Given a contingency table of dimensions r by c (rows x columns):
Calculate and fix the sizes of the marginal sums.
Calculate the total frequency, T, using the marginal sums.
Calculate the expected frequencies for each cell.
The general formula for obtaining the expected frequency of any cell xij, 1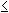 i
i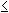 r, 1
r, 1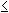 j
j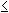 c in a contingency table is given by:
c in a contingency table is given by:
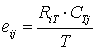
where RiT and CTj are the row total for ith row and the column total for jth column.
Select the test to be used to calculate 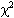 based on the highest expected frequency, m:
based on the highest expected frequency, m:
| if | then use |
m 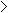 10 10 |
Chi-Square Test |
5 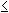 m m 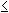 10 10 |
Yates' Correction for Continuity |
m 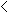 5 5 |
Fisher's Exact Test |
Calculate 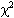 using the chosen test.
using the chosen test.
Calculate the degrees of freedom.
df = (r - 1)(c - 1)
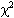 and df to determine if the conclusions are independent from the antecedent at the selected level of significance,
and df to determine if the conclusions are independent from the antecedent at the selected level of significance, 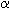 .
.Assume 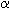 = 0.05 unless otherwise stated.
= 0.05 unless otherwise stated.
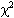
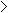
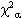
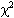
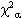
Chi-Square Formulae
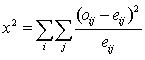
Yates' Correction for Continuity
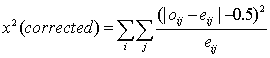
See Winston, pp. 437-442 for an explanation of Fisher's exact test.
Click here for an exercise in decision tree pruning.
Decision Lists
A decision list is a set of if-then statements.
It is searched sequentially for an appropriate if-then statement to be used as a rule.
 |
  |