| Dynamic Itemset Counting |
Su, Yibin, Dynamic Itemset Counting and Implication Rules for Market Basket Data: Project Final Report, CS831, April 2000.
Introduction
DIC Algorithm
Algorithm:
|
Itemset lattices: An itemset lattice contains all of the possible itemsets for a transaction database. Each itemset in the lattice points to all of its supersets. When represented graphically, a itemset lattice can help us to understand the concepts behind the DIC algorithm.
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
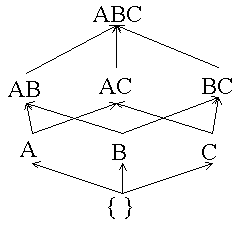 |
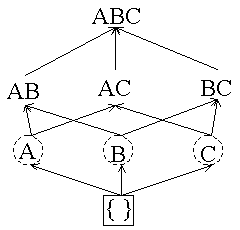 Empty itemset is marked with a solid box. All 1-itemsets are marked with dashed circles. |
|
After M transactions are read: 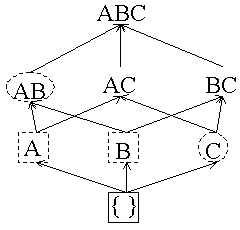 We change A and B to dashed boxes because their counters are greater than minsup (1) and add a counter for AB because both of its subsets are boxes. |
After 2M transactions are read: 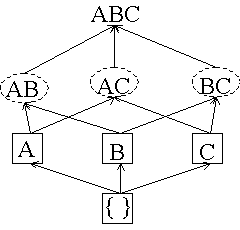 C changes to a square because its counter is greater than minsup.A, B and C have been counted all the way through so we stop counting them and make their boxes solid. Add counters for AC and BC because their subsets are all boxes. |
|
After 3M transactions read: 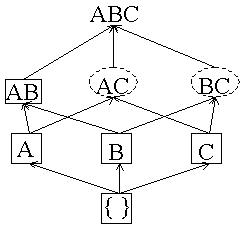 AB has been counted all the way through and its counter satisfies minsup so we change it to a solid box. BC changes to a dashed box. |
After 4M transactions read: 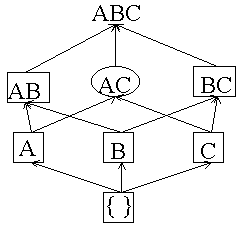 AC and BC are counted all the way through. We do not count ABC because one of its subsets is a circle. There are no dashed itemsets left so the algorithm is done. |
Implementation
Go to the DIC Implementation page to see a working implementation in Java.
Operations:
| SS = Æ ;
// solid square (frequent)
SC = Æ ; // solid circle (infrequent) DS = Æ ; // dashed square (suspected frequent) DC = { all 1-itemsets } ; // dashed circle (suspected infrequent) while (DS != 0) or (DC != 0) do begin read M transactions from database into T forall transactions t ÎT do begin //increment the respective counters of the itemsets marked with dash for each itemset c in DS or DC do begin if ( c Î t ) then c.counter++ ; for each itemset c in DC if ( c.counter ³ threshold ) then move c from DC to DS ; if ( any immediate superset sc of c has all of its subsets in SS or DS ) then add a new itemset sc in DC ; end for each itemset c in DS if ( c has been counted through all transactions ) then move it into SS ; for each itemset c in DC if ( c has been counted through all transactions ) then move it into SC ; end end Answer = { c Î SS } ; |