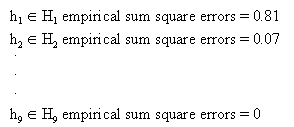Reference:
-
D. Schuurmans, Machine Learning course notes, University of Waterloo, 1999.
-
T. Mitchell, Machine Learning, McGraw-Hill, 1997, pp. 20-50.
Machine learning is a process which causes systems to improve with experience.
Elements of a Learning Task
Representation
- Items of Experience
- i
 I
I
- Space of Available Actions
- a
 A
A
- Evaluation
- Base Performance System
- b: I
 A
A
- Learning System
- L: (i1, a1, v1)...(in, an, vn)
 b
b
- Maps training experience sequence to base performance system.
Types of Learning Problems
Fundamental Distinctions
- Between problems rather than methods.
- Influences choice of method.
- Batch versus Online Learning:
- Batch Learning
- Training phase (no responsibility for performance during learning), then testing.
- Synthesizing a base performance system.
- Pure exploration.
- Online Learning
- No separate phase.
- Learning while doing.
- Have to decide between choosing actions to perform well now versus gaining knowledge to perform well later.
- Learning from Complete versus Partial Feedback:
- Complete Feedback
- Each item of experience evaluates every action (or base system).
- Tells what best action would have been.
- Partial Feedback
- Each item of experience evaluates only a subset of possible actions (or base systems).
- Only tells you how you did.
- Creates exploration/exploitation tradeoff in online setting.
- Should the reward be optimized with what is already known or should learning be attempted?
- In batch learning, exploration would be chosen since there is no responsibility for performance.
- Pointwise Feedback
- Evaluates single action.
- Optimization problem: (Controller, State)
 Action.
Action.
- Passive versus Active Learning
- Passive: observation.
- Active: experimentation, exploitation.
- Learning in Acausal versus Causal Situations
- Acausal: actions do not affect future experience.
- Causal: actions do effect future experience.
- Learning in Stationary versus Nonstationary Environments
- Stationary: evaluation doesn't change.
- Nonstationary: evaluation changes with time.
Concept Learning
The problem of inducing general functions from specific training examples is central to learning.
Concept learning acquires the definition of a general category given a sample of positive and negative training examples of the category, the method of which is the problem of searching through a hypothesis space for a hypothesis that best fits a given set of training examples.
A hypothesis space, in turn, is a predefined space of potential hypotheses, often implicitly defined by the hypothesis representation.
Learning a Function from Examples
- An example of concept learning where the concepts are mathematical functions.
Given:
- Domain X: descriptions
- Domain Y: predictions
- H: hypothesis space; the set of all possible hypotheses
- h: target hypothesis
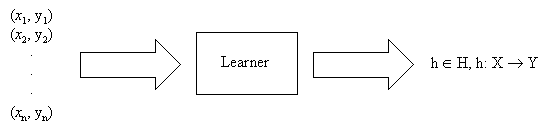
Idea: to extrapolate observed y's over all X.
Hope: to predict well on future y's given x's.
Require: there must be regularities to be found!
(Note type: batch, complete, passive (we are not choosing which x), acausal, stationary).
Many Research Communities
- Representation choice differs.
- Prefer maximum level of abstraction.
Traditional Statistics
- h: Rn
 R
R
- Squared prediction error.
- h is a linear function.
Traditional Pattern Recognition
- h: R
 {0, 1}
{0, 1}
- Right/wrong prediction error.
- h is a linear discriminant boundary.
"Symbolic" Machine Learning
- h: {attribute-value vectors}
 {0, 1}
{0, 1}
- h is a simple boolean function (eg. a decision tree).
Neural Networks
- h: Rn
 R
R
- h is a feedforward neural net.
Inductive Logic Programming
- h: {term structure}
 {0, 1}
{0, 1}
- h is a simple logic program.
Learning Theory
- Postulate mathematical model of learning situations.
- Rigorously establish achievable levels of learning performance.
- Characterize/quantify value of prior knowledge and constraints.
- Identify limits/possibilities of learning algorithms.
Standard Learning Algorithm
Given a batch set of training data S = {(x1, y1)...(xt, yt)}, consider a fixed hypothesis class H and compute a function h  H that minimizes empirical error.
H that minimizes empirical error.
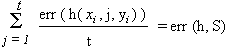
Example: Least-Squares Linear Regression
Here, the standard learning algorithm corresponds to least squares linear regression.
X = Rn, Y = R
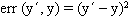
H = {linear functions Rn  R}
R}
Choosing a Hypothesis Space
In practice, for a given problem X  Y, which hypothesis space H do we choose?
Y, which hypothesis space H do we choose?

Question: since we know the true function f: X  Y, should we make H as "expressive" as possible and let the training data do the rest?
Y, should we make H as "expressive" as possible and let the training data do the rest?
- e.g., quadratic
- e.g., high degree polynomial
- e.g., complex neural network.
Answer: no!
Reason: overfitting!
- Underfit
- Unable to express a good prediction.
- Overfit
- Hard to identify good from bad candidates.
Basic Overfitting Phenomenon
Overfitting is bad.
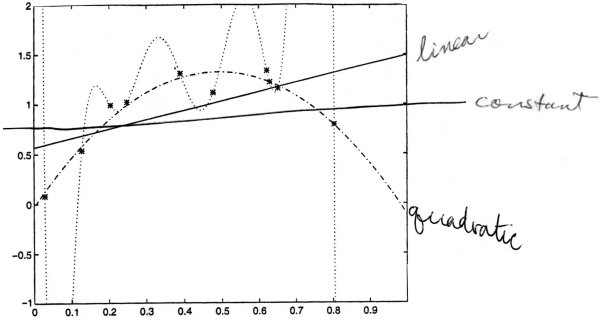
Example: polynomial regression
Suppose we use a hypothesis space, with many classes of functions

Given n = 10 training points (x1, y1)...(x10, y10).
Since n = 10, with 10 pieces of data, then in
Hn - 1 = H9
there is a function that gives an exact fit.
Which hypothesis would predict well on future examples?
- Although hypothesis h9 fits these 10 data exactly, it is unlikely to fit the next piece of data well.
When does empirical error minimization overfit?
Depends on the relationship between
- hypothesis class, H
- training sample size, t
- data generating process






 I
I A
A A
A b
b Action.
Action.
 R
R {0, 1}
{0, 1} {0, 1}
{0, 1} R
R {0, 1}
{0, 1} H that minimizes empirical error.
H that minimizes empirical error.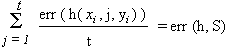
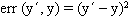
 R}
R} Y, which hypothesis space H do we choose?
Y, which hypothesis space H do we choose?
 Y, should we make H as "expressive" as possible and let the training data do the rest?
Y, should we make H as "expressive" as possible and let the training data do the rest?