Notes 06-3: Partitioning Methods (k-means)
Given a database of n objects and k, the number of clusters to generate, assign the objects into k partitions (k <= n), where each partition represents one cluster.
k-means Algorithm
The k-means algorithm is one of a group of algorithms called partitioning methods. The problem of partitional clustering can be formally stated as follows: Given n objects in a m-dimensional metric space, determine a partition of the objects into k groups, or clusters, such that the objects in a cluster are more similar to each other than to objects in different clusters. Recall that a partition divides a set into disjoint parts that together include all members of the set. The value of k may or may not be specified and a clustering criterion, typically the squared-error criterion, must be adopted.
The solution to this problem is straightforward. Select a clustering criterion, then for each data object select the cluster that optimizes the criterion. The k-means algorithm initializes k clusters by arbitrarily selecting one object to represent each cluster. Each of the remaining objects are assigned to a cluster and the clustering criterion is used to calculate the cluster mean. These means are used as the new cluster points and each object is reassigned to the cluster that it is most similar to. This continues until there is no longer a change when the clusters are recalculated. The algorithm is shown below.
k-means Algorithm:
1. Select k clusters arbitrarily.
2. Initialize cluster centers with those k clusters.
3. Do loop
a. Partition by assigning or reassigning all data objects to their closest cluster center.
b. Compute new cluster centers as mean value of the objects in each cluster.
Until no change in cluster center calculation
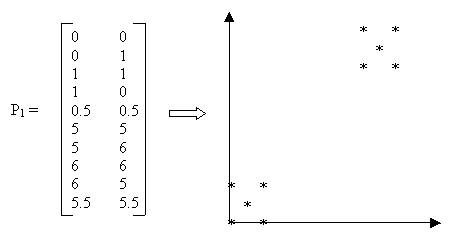
Figure 1: Sample Data
Example: Suppose we are given the data in Figure 1 as input and we choose k = 2 and the Manhattan distance function d = |x2 − x1| + |y2 − y1|. The detailed computation is as follows:
Step 1. Initialize k partitions. An initial partition can be formed by first specifying a set of k seed points. The seed points could be the first k objects or k objects chosen randomly from the input objects. We choose the first two objects as seed points and initialize the clusters as K1={(0,0)} and K2={(0,1)}.
Step 2. Since there is only one point in each cluster, that point is the cluster center.
Step 3a. Calculate the distance between each object and each cluster center, assigning the object to the closest cluster.
For example, for the third object:
d(1,3) = |1 − 0| + |1 − 0| = 2 and
d(2,3) = |1 − 0| + |1 − 1| = 1,
so this object is assigned to K2.
The fifth object is equidistant from both clusters, so we arbitrarily assign it to K1.
After calculating the distance for all points, the clusters contain the following objects:
K1 = {(0,0),(1,0),(0.5,0.5)} and
K2 = {(0,1),(1,1),(5,5),(5,6),(6,6),(6,5),(5.5,5.5)}.
Step 3b. Compute new cluster center for each cluster.
New center for K1 is C1 = (0.5,0.16)
(0+1+0.5)/3 = 0.5
(0+0+0.5)/3 = 0.16
New center for K2 is C2 = (4.1,4.2)
(0+1+5+5+6+6+5.5)/7 = 4.1
(1+1+5+5+6+6+5.5)/7 = 4.2
Step 3a'. New centers C1 = (0.5,0.16) and C2 = (4.1,4.2) differ from old centers C1 = (0,0) and C2 = (0,1), so the loop is repeated.
Reassign the ten objects to the closest cluster center, resulting in:
K1 = {(0,0),(0,1),(1,1),(1,0),(0.5,0.5)}
K2 = {(5,5),(5,6),(6,6),(6,5),(5.5,5.5)}
Step 3b'. Compute new cluster center for each cluster
New center for K1 is C1 = (0.5,0.5)
New center for K2 is C2 = (5.5,5.5)
Step 3a''. New centers C1 = (0.5,0.5) and C2 = (5.5,5.5) differ from old centers C1 = (0.5,0.16) and C2 = (4.1,4.2), so the loop is repeated.
Reassign the ten objects to the closest cluster center. Result is same as in Step 3a'.
Step 3b''. Compute new cluster centers.
Algorithm is done: Centers are the same as in Step 3b', so algorithm is finished. Result is same as in 3b'.
The k-means method assigns objects into clusters so that the resulting intra-cluster similarity is high, but the inter-cluster similarity is low.
The k-means method (a centroid-based approach)
Algorithm: k-Means
Input: k = the number of clusters to generate
D = a set of n instances of the form (p1, p2, …, pm), where each pu represents a coordinate in a m-dimensional space
Output: K = a set of k clusters
Method:
1. arbitrarily choose k instances as the initial centroids
2. repeat
3. assign each remaining instance to the cluster Ka to which it is most similar (i.e., to the same cluster as the centroid to which it is closest)
4. determine the new centroid for each cluster Ka based upon the instances currently assigned to Ka
5. until no change in the centroid of each Ka from the previous iteration of the loop
Advantages of k-means clustering:
· The method is relatively scalable and efficient in processing large datasets and has computational complexity of O(nkt), where n is the number of instances, k is the number of clusters, and t is the number of iterations.
· Often terminates at a local optimum.
Disadvantages of k-means clustering:
· Only applicable when the mean of a cluster is defined (i.e., categorical attributes don’t work).
· Need to specify k in advance.
· Doesn’t work well when there is a “large” difference in the size of the clusters.
· Sensitive to noise and outliers.
k-medioids
It turns out that using medoids (i.e., the most centrally located instance in a cluster) is less sensitive to outliers than when the mean value of the instances is used (the basis of the k-means method).
The basic strategy of the k-medoids method is to find k clusters from n instances by finding a representative instance (i.e., the medoid) for each cluster.
An instance is clustered with the medoid to which it is most similar.
Medoids are then iteratively replaced by non-medoids as long as the quality of the resulting clusters is improved.
To determine whether a non-medoid instance is a “good” replacement for a medoid, four cases are evaluated (assume ma and mb are medoids, mcandidate is a candidate medoid, and p is a non-medoid object):
· Case 1: Instance p is clustered with ma. If ma is replaced by mcandidate and p is closest to some mb, a ≠ b, then p is clustered with mb.
· Case 2: Instance p is clustered with ma. If ma is replaced by mcandidate and p is closest to mcandidate, then p is clustered with mcandidate.
· Case 3: Instance p is clustered with ma. If mb, a ≠ b, is replaced by mcandidate and p is still closest to ma, then p remains clustered with ma.
· Case 4: Instance p is clustered with ma. If mb, a ≠ b, is replaced by mcandidate and p is closest to mcandidate, then p is clustered with mcandidate.
The k-medoids method (a representative object-based approach)
Algorithm: k-Medoids
Input: k = the number of clusters to generate
D = a set of n instances of the form (p1, p2, …, pm), where each pu represents a coordinate in a m-dimensional space
Output: K = a set of k clusters that minimizes the sum of the dissimilarities of all objects to their nearest medoid
Method:
1. arbitrarily choose k instances as the initial medoids
2. repeat
3. assign each non-medoid instance to the cluster Ka to which it is most similar (i.e., to the same cluster as the medoid to which it is closest)
4. determine the current total cost for the clusters (i.e., the summation of the distance from each instance to its medoid)
5. randomly select a non-medoid instance as the candidate medoid
6. iteratively swap the medoid of each cluster Ka with the candidate medoid and determine the total cost for the clusters
7. use the clusters from the iteration that has the minimal total cost (one cluster from this iteration, Kcandidate, will have the candidate medoid as its medoid)
8. if minimal total cost – current total cost < 0
9. make the candidate medoid the new medoid for Kcandidate
10. until no change in the medoid of each cluster Ka from the previous iteration of the loop
Example – k-medoids clustering a two-dimensional dataset
|
Instance |
x |
y |
|
1 |
2 |
3 |
|
2 |
2 |
6 |
|
3 |
3 |
5 |
|
4 |
3 |
8 |
|
5 |
4 |
7 |
|
6 |
6 |
2 |
|
7 |
6 |
4 |
|
8 |
7 |
3 |
|
9 |
7 |
4 |
|
10 |
7 |
6 |
Assume k = 2 and the use of the Manhattan distance function.
Step 1: Arbitrarily choose instances 2 and 5 as the initial medoids, denoted m1 and m2, respectively. So, m1 = (2, 6) and m2 = (4, 7).
Step 3: Calculate the distance between each instance and the initial medoids…
d(m1,1) = d(2,1) = |2 – 2| + |6 – 3| = 3 1 is closer to m1
d(m2,1) = d(5,1) = |4 – 2| + |7 – 3| = 6
d(m1,3) = d(2,3) = |2 – 3| + |6 – 5| = 2 3 is closer to m1
d(m2,3) = d(5,3) = |4 – 3| + |7 – 5| = 3
d(m1,4) = d(2,4) = |2 – 3| + |6 – 8| = 3
d(m2,4) = d(5,4) = |4 – 3| + |7 – 8| = 2 4 is closer to m2
d(m1,6) = d(2,6) = |2 – 6| + |6 – 2| = 8
d(m2,6) = d(5,6) = |4 – 6| + |7 – 2| = 7 6 is closer to m2
d(m1,7) = d(2,7) = |2 – 6| + |6 – 4| = 6
d(m2,7) = d(5,7) = |4 – 6| + |7 – 4| = 5 7 is closer to m2
d(m1,8) = d(2,8) = |2 – 7| + |6 – 3| = 8
d(m2,8) = d(5,8) = |4 – 7| + |7 – 3| = 7 8 is closer to m2
d(m1,9) = d(2,9) = |2 – 7| + |6 – 4| = 7
d(m2,9) = d(5,9) = |4 – 7| + |7 – 4| = 6 9 is closer to m2
d(m1,10) = d(2,10) = |2 – 7| + |6 – 6| = 5
d(m2,10) = d(5,10) = |4 – 7| + |7 – 6| = 4 10 is closer to m2
and assign each instance to the same cluster as the medoid to which it is closest. Thus,
K1 = {1, 2, 3} = {(2, 3), (2, 6), (3, 5)}
K2 = {4, 5, 6, 7, 8, 9, 10} = {(3, 8), (4, 7), (6, 2), (6, 4), (7, 3), (7, 4), (7, 6)}
Step 4: Determine the current total cost for the clusters.
|
current total cost |
= d(2, 1) + d(2, 3) + d(5, 4) + d(5, 6) + d(5, 7) + d(5, 8) + d(5, 9) + d(5, 10) = 3 + 2 + 2 + 7 + 5 + 7 + 6 + 4 = 36 |
Step 5: Select (randomly) instance 9 as the candidate medoid.
Step 6: Iteratively swap the medoid of each cluster with the candidate medoid. Swap m1 (i.e., instance 2) and instance 9.
d(m1c,1) = d(9,1) = 6 equidistant from m1 and m2 so,
d(m2,1) = d(5,1) = 6 pick one, say m2
d(m1c,2) = d(9,2) = 7
d(m2,2) = d(5,2) = 3 2 is closer to m2
d(m1c,3) = d(9,3) = 5
d(m2,3) = d(5,3) = 3 3 is closer to m2
d(m1c,4) = d(9,4) = 8
d(m2,4) = d(5,4) = 2 4 is closer to m2
d(m1c,6) = d(9,6) = 4 6 is closer to candidate
d(m2,6) = d(5,6) = 7
d(m1c,7) = d(9,7) = 1 7 is closer to candidate
d(m2,7) = d(5,7) = 5
d(m1c,8) = d(9,8) = 1 8 is closer to candidate
d(m2,8) = d(5,8) = 6
d(m1c,10) = d(9,10) = 2 10 is closer to candidate
d(m2,10) = d(5,10) = 4
Total cost when instances 2 and 9 are swapped is
|
total cost |
= d(5, 1) + d(5, 2) + d(5, 3) + d(5, 4) + d(9, 6) + d(9, 7) + d(9, 8) + d(9, 10) = 6 + 3 + 3 + 2 + 4 + 1 + 1 + 2 = 22 |
Swap m2 (i.e., instance 5) and instance 9.
d(m1,1) = d(2,1) = 3 1 is closer to m1
d(m2c,1) = d(9,1) = 6
d(m1,3) = d(2,3) = 2 3 is closer to m1
d(m2c,3) = d(9,3) = 5
d(m1,4) = d(2,4) = 3 4 is closer to m1
d(m2c,4) = d(9,4) = 8
d(m1,5) = d(2,5) = 3 5 is closer to m1
d(m2c,5) = d(9,5) = 6
d(m1,6) = d(2,6) = 8
d(m2c,6) = d(9,6) = 3 6 is closer to candidate
d(m1,7) = d(2,7) = 6
d(m2c,7) = d(9,7) = 1 7 is closer to candidate
d(m1,8) = d(2,8) = 8
d(m2c,8) = d(9,8) = 1 8 is closer to candidate
d(m1,10) = d(2,10) = 5
d(m2c,10) = d(9,10) = 2 10 is closer to candidate
Total cost when instances 2 and 9 are swapped is
|
total cost |
= d(2, 1) + d(2, 3) + d(2, 4) + d(2, 5) + d(9, 6) + d(9, 7) + d(9, 8) + d(9, 10) = 3 + 2 + 3 + 3 + 3 + 1 + 1 + 2 = 18 |
Step 7: The minimal total cost for the clusters was obtained when instances 5 and 9 were swapped in K2. That is, when instance 9 was the candidate medoid.
Step 8: Since minimal total cost – current total cost = 18 – 36 = –18, and –18 < 0, make instance 9 the new medoid for K2.
Step 3: Assign each instance to the same cluster as the medoid to which it is closest. Thus,
K1 = {1, 2, 3, 4, 5} = {(2, 3), (2, 6), (3, 5), (3, 8), 4, 7)}
K2 = {6, 7, 8, 9, 10} = {(6, 2), (6, 4), (7, 3), (7, 4), (7, 6)}
Step 4: Determine the current total cost for the clusters.
|
current total cost |
= d(2, 1) + d(2, 3) + d(2, 4) + d(2, 5) + d(9, 6) + d(9, 7) + d(9, 8) + d(9, 10) = 3 + 2 + 3 + 3 + 3 + 1 + 1 + 2 = 18 |
Step 5: Select (randomly) instance 3 as the candidate medoid.
Step 6: Iteratively swap the medoid of each cluster with the candidate medoid. Swap m1 (ie. instance 2) and instance 3 and re-calculate the total cost (details not shown). Total cost when instances 2 and 3 are swapped is
total cost = 19
Swap m2 (i.e., instance 9) and instance 3 and re-calculate the total cost (details not shown). Total cost when instances 9 and 3 are swapped is
total cost = 35
Step 7: The minimal total cost for the clusters was obtained when instances 2 and 3 were swapped in K1. That is, when instance 3 was the candidate medoid.
Step 8: Since minimal total cost – current total cost = 19 – 18 = 1, and 1 > 0, then instance 3 (i.e., the candidate medoid) does not replace instance 2 as the medoid of K1.
Step 10: The medoids are the same as the previous iteration, so K = {K1, K2} = {{1, 2, 3, 4, 5}, {6, 7, 8, 9, 10}}.
Disadvantage of k-medoids clustering is computational complexity:
For each iteration, there are k(n – k) pairs of objects for which the distance must be determined.
Calculating the distance to all other non-medoids during each iteration is done n – k times.
So, total complexity per iteration is O(k(n – k)(n – k)) = O(n2).
The CLARA (Clustering LARge Applications) method improves on the complexity of the k-medoids method by sampling instances from the database and selecting medoids from the sample before assigning all instances to clusters.
To increase accuracy, several samples can be drawn and the k-medoids method can be applied to each, with the clusters having the lowest cost selected for the next iteration.
The CLARA method
Algorithm: CLARA
Input: k = the number of clusters to generate
D = a set of n instances of the form (p1, p2, …, pm), where each pu represents a coordinate in a m-dimensional space
r = the number of times to draw samples and cluster
Output: bestK = a set of k clusters that minimizes the sum of the dissimilarities of all objects to their nearest medoid
Method:
1. set minimum cost to HIGH_VALUES (i.e., some large number)
2. r = 5 (i.e., some arbitrary number of times to repeat sampling and clustering)
3. repeat r times
4. select 40 + 2 * k instances from D to create S (i.e., the current sample)
5. K = k-Medoids (k, S)
6. current cost = Cost (K, D)
7. if current cost < minimum cost
8. minimum cost = current cost
9. bestK = K
Algorithm: Cost
Input: K = a set of k medoids
D = a set of n instances
Output: average cost = the average cost from every object in D and the medoid to which it is closest
1. for j = 1 to n
2. iteratively determine the cost from j to each medoid Ka
3. use the cost from the iteration that has the minimal cost
4. total cost = total cost + minimal cost
5. average cost = total cost / n
Since CLARA adopts a sampling approach, the quality of its clusters depends on the size of the sample.
When the sample size is small and the dataset is large, the quality of the clusters may not be good.
It has been shown experimentally that drawing five samples of size 40 + 2k seems to give “good” results.
Total complexity per iteration is O(ks2 + k(n – k)), where k is the number of clusters, n is the number of instances, and s is the sample size.