Notes 06-4: Hierarchical Methods
Hierarchical algorithms can be either agglomerative or divisive, that is top-down or bottom-up. All agglomerative hierarchical clustering algorithms begin with each object as a separate group. These groups are successively combined based on similarity until there is only one group remaining or a specified termination condition is satisfied. For n objects, n−1 mergings are done. Hierarchical algorithms are rigid in that once a merge has been done, it cannot be undone. Although there are smaller computational costs with this, it can also cause problems if an erroneous merge is done. As such, merge points need to be chosen carefully. Here we describe a simple agglomerative clustering algorithm. More complex algorithms have been developed, such as BIRCH and CURE, in an attempt to improve the clustering quality of hierarchical algorithms.
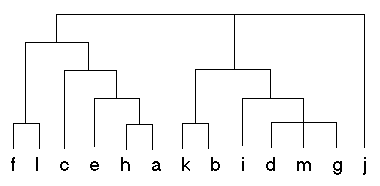
Figure 1: Sample Dendogram
In the context of hierarchical clustering, the hierarchy graph is called a dendogram. Figure 1 shows a sample dendogram that could be produced from a hierarchical clustering algorithm. Unlike with the k-means algorithm, the number of clusters (k) is not specified in hierarchical clustering. After the hierarchy is built, the user can specify the number of clusters required, from 1 to n. The top level of the hierarchy represents one cluster, or k=1. To examine more clusters, we simply need to traverse down the hierarchy.
A hierarchical method creates a hierarchical decomposition (using a top-down approach) or a hierarchical composition (using a bottom-up approach) that groups instances using a tree.
AGNES Method
The AGNES (AGglomerative NESting) method builds a hierarchy graph called a dendogram.
Each instance is initially assigned to its own cluster (i.e., each cluster contains a single instance).
The clusters are merged into new clusters (i.e., creating nodes at lower levels in the graph) until there is only one cluster containing all the instances.
DIAGRAM = Clustering.F.1.b
The similarity between two clusters is measured by the similarity of the closest pair of instances.
The two clusters may be merged if the distance between two instances is the minimum between any two instances from all the clusters.
The distance between two instances can be determined using any similarity or distance measures.
Unlike the partitioning methods, the number of clusters is not specified.
After the hierarchy is built, the user can specify the number of clusters required (i.e., from 1 to n).
The top level represents n clusters (or k = n) and fewer clusters (i.e., k < n) can be obtained by descending the hierarchy.
The AGNES method (a hierarchical composition approach)
Algorithm: AGNES
Input: D = a set of n instances of the form (p1, p2, …, pm), where each pu represents a coordinate in a m-dimensional space
Output: K = a nested set of instances (i.e., implicitly representing the hierarchy of clusters)
Method:
1. for i = 1 to n
2. Ki = {i} (i.e., instance i)
3. K = {K1, K2, …, Kn} (i.e., K is a set of single-element sets)
4. c = n + 1
5. while |K| > 1
6. determine the distance between all pairs of instances i and j from different clusters in K
7. use the pair of clusters associated with the instances i and j that have the minimum distance (call them Kmin1 and Kmin2, respectively)
8. remove Kmin1 and Kmin2 from K
9. insert Kc = { Kmin1, Kmin2} into K
10. c ++
Agglomerative clustering methods suffer from a few of major weaknesses:
· The complexity is at least O(n2), so it does not scale well to large datasets.
· Once two clusters are combined, the algorithm cannot split the resulting cluster if it turns out to be a bad decision.
· Once two clusters are combined, the algorithm cannot swap instances between clusters to further improve the resulting clusters.
Example – Agglomerative nested clustering of a two-dimensional dataset
|
Instance |
x |
y |
|
1 |
0 |
0 |
|
2 |
1 |
1 |
|
3 |
3 |
1 |
|
4 |
2 |
4 |
|
5 |
6 |
3 |
|
6 |
6 |
6 |
|
7 |
5 |
2 |
|
8 |
3 |
5 |
|
9 |
0 |
2 |
|
10 |
2 |
1 |
Assume the use of the Manhattan distance function.
Steps 1 to 3: Assign each instance to its own cluster. For example, K1 = {1}, K2 = {2}, …, K10 = {10}. Thus,
K = {{1}, {2}, {3}, {4}, {5}, {6}, {7}, {8}, {9}, {10}}.
Step 5: | K | = 10, so continue.
Step 6: Determine the distance between all pairs of instances from different clusters in K (not shown).
Step 7: The minimum distance between two pairs of instances is 1, occurring between instances 2 and 10 and instances 3 and 10. Arbitrarily choose instances 2 and 10. Thus, Kmin1 = K2 = {2} and Kmin2 = K10 = {10}.
Step 8: Remove Kmin1 and Kmin2 from K. Thus,
K = {{1}, {3}, {4}, {5}, {6}, {7}, {8}, {9}}.
Step 9: Insert K11 = {{2}, {10}} into K. Thus,
K = {{1}, {3}, {4}, {5}, {6}, {7}, {8}, {9}, {{2}, {10}}}.
Step 5: | K | = 9, so continue.
Step 6: Determine the distance between all pairs of instances from different clusters in K (not shown).
Step 7: The minimum distance between two pairs of instances is 1, occurring between instances 3 and 10. Thus, Kmin1 = K3 = {3} and Kmin2 = K11 = {{2}, {10}}.
Step 8: Remove Kmin1 and Kmin2 from K. Thus,
K = {{1}, {4}, {5}, {6}, {7}, {8}, {9}}.
Step 9: Insert K12 = {{{2}, {10}}, {3}} into K. Thus,
K = {{1}, {4}, {5}, {6}, {7}, {8}, {9}, {{{2}, {10}}, {3}}}.
Step 5: | K | = 8, so continue.
Note: From here on, not all steps are shown.
Step 7: Kmin1 = K1 = {1} and Kmin2 = K12 = {{{2}, {10}}, {3}}.
Step 9: Insert K13. Thus,
K = {{4}, {5}, {6}, {7}, {8}, {9}, {{{{2}, {10}}, {3}}, {1}}}.
Step 5: | K | = 7, so continue.
Step 7: Kmin1 = K4 = {4} and Kmin2 = K8 = {8}.
Step 9: Insert K14. Thus,
K = {{5}, {6}, {7}, {9}, {{{{2}, {10}}, {3}}, {1}}, {{4}, {8}}}.
Step 5: | K | = 6, so continue.
Step 7: Kmin1 = K5 = {5} and Kmin2 = K7 = {7}.
Step 9: Insert K15. Thus,
K = {{6}, {9}, {{{{2}, {10}}, {3}}, {1}}, {{4}, {8}}, {{5}, {7}}}.
Step 5: | K | = 5, so continue.
Step 7: Kmin1 = K9 = {9} and Kmin2 = K13 = {{{{2}, {10}}, {3}}, {1}}.
Step 9: Insert K16. Thus,
K = {{6}, {{4}, {8}}, {{5}, {7}}, {{{{{2}, {10}}, {3}}, {1}}, {9}}}.
Step 5: | K | = 4, so continue.
Step 7: Kmin1 = K6 = {6} and Kmin2 = K15 = {{5}, {7}}.
Step 9: Insert K17. Thus,
K = {{{4}, {8}}, {{{{{2}, {10}}, {3}}, {1}}, {9}}, {{{5}, {7}}, {6}}}.
Step 5: | K | = 3, so continue.
Step 7: Kmin1 = K14 = {{4}, {8}} and Kmin2 = K16 = {{{{{2}, {10}}, {3}}, {1}}, {9}}.
Step 9: Insert K18. Thus,
K = {{{{5}, {7}}, {6}}, {{{{{{2}, {10}}, {3}}, {1}}, {9}}, {{4}, {8}}}}.
Step 5: | K | = 2, so continue.
Step 7: Kmin1 = K17 = {{{5}, {7}}, {6}} and Kmin2 = K18 = {{{{{{2}, {10}}, {3}}, {1}}, {9}}, {{4}, {8}}}.
Step 9: Insert K19. Thus,
K = {{{{{{{{2}, {10}}, {3}}, {1}}, {9}}, {{4}, {8}}}, {{{5, {7}}, {6}}}}.
Step 5: | K | = 1, so stop.
K is the nested set of clusters shown in the following diagram.
DIAGRAM = Clustering.F.1.e
DIANA Method
The DIANA (DIvisive ANAlysis) method is like a reverse AGNES method.
All data are initially assigned to one cluster.
At each step, the cluster with the largest diameter is divided into two new clusters until all clusters contain only one instance.
DIAGRAM = Clustering.F.2.b
The DIANA method (a hierarchical decomposition approach)
Algorithm: DIANA
Input: D = a set of n instances of the form (p1, p2, …, pm), where each pu represents a coordinate in a m-dimensional space
Output: K = a nested set of instances (i.e., implicitly representing the hierarchy of clusters)
Method:
1. K0 = {D} (i.e., K0 contains all the instances in D)
2. K = {K0}
3. a = 0
4. while there is a cluster K' ∈ K such that |Kb|>1
5. determine the diameter of each cluster
6. let cluster K' be the cluster with the largest diameter
7. a ++
8. if |K'| == 2
9. arbitrarily select h from the two instances in K'
10. Ka = {h}
11. K = K ∪ Ka
12. K' = K' – h (i.e., h is removed from K')
13. else
14. Ka = {}
15. K = K ∪ Ka
16. determine the average distance between all pairs of instances i and j in cluster K'
17. use the instance h that has the greatest average distance
18. Ka = Ka ∪ h (i.e., h in Ka is the initial instance in a new cluster)
19. K' = K' − h (i.e., h is removed from K')
20. repeat
21. for each instance i ∉ Ka (i.e., where instance i is not in the new cluster)
22. average outside distance = Costj∉Ka (i, j) (i.e., the average distance between instance i outside Ka and all instances j outside Ka)
23. average inside distance = Costj∈Ka (i, j) (i.e., the average distance between instance i outside Ka and all instances j inside Ka)
24. net distance = average outside distance – average inside distance
25. use the instance h that has the greatest net distance
26. if the net distance for instance h > 0
27. Ka = Ka ∪ h (i.e., h is another instance that can be added to Ka)
28. K' = K' − h (i.e., h is removed from K')
29. until all net distances for each instance are < 0
Example – divisive analysis of a two-dimensional dataset
|
Instance |
x |
y |
|
1 |
2 |
2 |
|
2 |
5.5 |
4 |
|
3 |
5 |
5 |
|
4 |
1.5 |
2.5 |
|
5 |
1 |
1 |
|
6 |
7 |
5 |
|
7 |
5.75 |
6.5 |
In this example, the data is standardized (for no particular reason) by finding the z-score, resulting in the table shown below.
|
Instance |
x |
y |
|
1 |
-0.82 |
-0.88 |
|
2 |
0.64 |
0.15 |
|
3 |
0.43 |
0.66 |
|
4 |
-1.03 |
-0.62 |
|
5 |
-1.24 |
-1.39 |
|
6 |
1.26 |
0.66 |
|
7 |
0.74 |
1.43 |
Assume the use of the Euclidean distance function. Also, assume that the distance between all pairs of points in D has been calculated and stored in a proximity matrix, resulting in the table shown below (these values will be used frequently in the steps that follow.
|
Instance |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
|
1 |
0.00 |
1.78 |
1.98 |
0.33 |
0.66 |
2.59 |
2.78 |
|
2 |
1.78 |
0.00 |
0.55 |
1.83 |
2.42 |
0.81 |
1.28 |
|
3 |
1.98 |
0.55 |
0.00 |
1.94 |
2.64 |
0.83 |
0.83 |
|
4 |
0.33 |
1.83 |
1.94 |
0.00 |
0.80 |
2.62 |
2.71 |
|
5 |
0.66 |
2.42 |
2.64 |
0.80 |
0.00 |
3.23 |
3.44 |
|
6 |
2.59 |
0.81 |
0.83 |
2.62 |
3.23 |
0.00 |
0.93 |
|
7 |
2.78 |
1.28 |
0.83 |
2.71 |
3.44 |
0.93 |
0.00 |
Steps 1 and 2: Assign all instances to one cluster. For example, let K0 = {1, 2, 3, 4, 5, 6, 7}.
K = {K0} = {{1, 2, 3, 4, 5, 6, 7}}.
Step 3: Initialize a (i.e., the cluster counter).
Step 4: |K0| > 1, so continue.
Step 5: Determine the diameter of each cluster containing more than one instance. However, at this point, there is only one cluster, namely, K0, so…
Step 6: Use K0.
Step 7: Increment a.
Step 8: Since |K0| > 2, go to Step 14.
Steps 14 and 15: K1 = {} and K = K ∪ K1. Thus,
K = {{1, 2, 3, 4, 5, 6, 7}, {}}.
Step 16: Calculate the average distance between all pairs of instances in K0. For example, the values used to calculate the average for instance 1 correspond to the distances from instance 1 to instances 2 (i.e., 1.78), 3 (i.e., 1.98), 4 (i.e., 033), 5 (i.e., 0.66), 6 (i.e., 2.59), and 7 (i.e., 2.78).
|
Instance |
Average Distance to Other Instances |
|
1 |
(1.78 + 1.98 + 0.33 + 0.66 + 2.59 + 2.78) / 6 = 1.69 |
|
2 |
(1.78 + 0.55 + 1.83 + 2.42 + 0.81 + 1.28) / 6 = 1.45 |
|
3 |
(1.98 + 0.55 + 1.94 + 2.64 + 0.83 + 0.83) / 6 = 1.46 |
|
4 |
(0.33 + 1.83 + 1.94 + 0.80 + 2.62 + 2.71) / 6 = 1.71 |
|
5 |
(0.66 + 2.42 + 2.64 + 0.80 + 3.23 + 3.44) / 6 = 2.20 |
|
6 |
(2.59 + 0.81 + 0.83 + 2.62 + 3.23 + 0.93) / 6 = 1.84 |
|
7 |
(2.78 + 1.28 + 0.83 + 2.71 + 3.44 + 0.93) / 6 = 2.00 |
Step 17: Instance 5 has the greatest average distance (i.e., it is least similar to the other instances).
Steps 18 and 19: K1 = K1 ∪ 5 and K0 = K0 − 5. Thus,
K = {{1, 2, 3, 4, 6, 7}, {5}}.
Steps 21 to 24: Calculate the average distance from each instance inside K0 to the other instances inside K0, and calculate the average distance from each instance inside K0 to the instances inside K1.
|
Instance |
Average Distance Inside K0 |
Average Distance Inside K1 |
Net Distance |
|
1 |
(1.78 + 1.98 + 0.33 + 2.59 + 2.78) / 5 = 1.89 |
0.66 |
1.23 |
|
2 |
(1.78 + 0.55 + 1.83 + 0.81 + 1.28) / 5 = 1.25 |
2.42 |
-1.17 |
|
3 |
(1.98 + 0.55 + 1.94 + 0.83 + 0.83) / 5 = 1.23 |
2.64 |
-1.41 |
|
4 |
(0.33 + 1.83 + 1.94 + 2.62 + 2.71) / 5 = 1.89 |
0.80 |
1.09 |
|
6 |
(2.59 + 0.81 + 0.83 + 2.62 + 0.93) / 5 = 1.56 |
3.23 |
-1.67 |
|
7 |
(2.78 + 1.28 + 0.83 + 2.71 + 0.93) / 5 = 1.71 |
3.44 |
-1.73 |
Step 25: Instance 1 has the greatest net distance.
Step 26: 1.23 > 0, so…
Steps 27 and 28: K1 = K1 ∪ 1 and K0 = K0 − 1. Thus,
K = {{2, 3, 4, 6, 7}, {1, 5}}.
Step 29: Not all net distances are < 0, so continue at Step 20.
Steps 21 to 24: Calculate the average distance from each instance inside K0 to the other instances inside K0, and calculate the average distance from each instance inside K0 to the instances inside K1.
|
Instance |
Average Distance Inside K0 |
Average Distance Inside K1 |
Net Distance |
|
2 |
(0.55 + 1.83 + 0.81 + 1.28) / 4 = 1.12 |
(1.78 + 2.42) / 2 = 2.10 |
-0.98 |
|
3 |
(0.55 + 1.94 + 0.83 + 0.83) / 4 = 1.04 |
(1.98 + 2.64) / 2 = 2.31 |
-1.27 |
|
4 |
(1.83 + 1.94 + 2.62 + 2.71) / 4 = 2.28 |
(0.33 + 0.80) /2 = 0.56 |
1.72 |
|
6 |
(0.81 + 0.83 + 2.62 + 0.93) / 4 = 1.30 |
(2.59 + 3.23) / 2 = 2.91 |
-1.61 |
|
7 |
(1.28 + 0.83 + 2.71 + 0.93) / 4 = 1.44 |
(2.78 + 3.44) / 2 = 3.11 |
-1.67 |
Step 25: Instance 4 has the greatest net distance.
Step 26: 1.71 > 0, so…
Steps 27 and 28: K1 = K1 ∪ 4 and K0 = K0 − 4. Thus,
K = {{2, 3, 6, 7}, {1, 4, 5}}.
Step 29: Not all net distances are < 0, so continue at Step 20.
Steps 21 to 24: Calculate the average distance from each instance inside K0 to the other instances inside K0, and calculate the average distance from each instance inside K0 to the instances inside K1.
|
Instance |
Average Distance Inside K0 |
Average Distance Inside K1 |
Net Distance |
|
2 |
(0.55 + 0.81 + 1.28) / 3 = 0.88 |
(1.78 + 1.83 + 2.42) / 3 = 2.01 |
-1.13 |
|
3 |
(0.55 + 0.83 + 0.83) / 3 = 0.74 |
(1.98 + 1.94 + 2.64) / 3 = 2.19 |
-1.45 |
|
6 |
(0.81 + 0.83 + 0.93) / 3 = 0.86 |
(2.59 + 2.62 + 3.23) / 3 = 2.81 |
-1.96 |
|
7 |
(1.28 + 0.83 + 0.93) / 3 = 1.01 |
(2.78 + 3.44 + 2.71) / 3 = 2.98 |
-1.96 |
Step 25: Instance 2 has the greatest net distance, but…
Step 26: -1.13 < 0, so continue at Step 29.
Step 29: All net distances are < 0, so continue at Step 4.
Step 4: |K0| > 1 and |K1| > 1, so continue.
Step 5: Determine the diameter of each cluster containing more than one instance.
Step 6: The diameter of K0 and K1 is 1.28 and 0.80, respectively. Use K0 because it is largest.
Step 7: Increment a.
Step 8: Since |K0| > 2, go to Step 14.
Steps 14 and 15: K2 = {} and K = K ∪ K2. Thus,
K = {{2, 3, 6, 7}, {1, 4, 5}, {}}.
Step 16: Calculate the average distance between all pairs of instances in K0.
|
Instance |
Average Distance to Other Instances |
|
2 |
(0.55 + 0.81 + 1.28) / 3 = 0.88 |
|
3 |
(0.55 + 0.83 + 0.83) / 3 = 0.74 |
|
6 |
(0.81 + 0.83 + 0.93) / 3 = 0.86 |
|
7 |
(1.28 + 0.83 + 0.93) / 3 = 1.01 |
Step 17: Instance 7 has the greatest average distance (i.e., it is least similar to the other instances).
Steps 18 and 19: K2 = K2 ∪ 7 and K0 = K0 − 7. Thus,
K = {{2, 3, 6}, {1, 4, 5}, {7}}.
Steps 21 to 24: Calculate the average distance from each instance inside K0 to the other instances inside K0, and calculate the average distance from each instance inside K0 to the instances inside K2.
|
Instance |
Average Distance Inside K0 |
Average Distance Inside K2 |
Net Distance |
|
2 |
(0.55 + 0.81) / 2 = 0.68 |
1.28 |
-0.60 |
|
3 |
(0.55 + 0.83) / 2 = 0.69 |
0.83 |
-0.14 |
|
6 |
(0.81 + 0.83) / 2 = 0.82 |
0.93 |
-0.11 |
Step 25: Instance 6 has the greatest net distance, but …
Step 26: -0.11 < 0, so continue at Step 29.
Step 29: All net distances are < 0, so continue at Step 4.
Step 4: |K0| > 1 and |K1| > 1, so continue.
Step 5: Determine the diameter of each cluster containing more than one instance.
Step 6: The diameter of K0 and K1 is 0.83 and 0.80, respectively. Use K0 because it is largest.
Step 7: Increment a.
Step 8: Since |K0| > 2, go to Step 14.
Steps 14 and 15: K3 = {} and K = K ∪ K3. Thus,
K = {{2, 3, 6}, {1, 4, 5}, {7}, {}}.
Step 16: Calculate the average distance between all pairs of instances in K0.
|
Instance |
Average Distance to Other Instances |
|
2 |
(0.55 + 0.81) / 2 = 0.68 |
|
3 |
(0.55 + 0.83) / 2 = 0.69 |
|
6 |
(0.81 + 0.83) / 2 = 0.82 |
Step 17: Instance 6 has the greatest average distance (i.e., it is least similar to the other instances).
Steps 18 and 19: K3 = K3 ∪ 6 and K0 = K0 − 6. Thus,
K = {{2, 3}, {1, 4, 5}, {7}, {6}}.
Steps 21 to 24: Calculate the average distance from each instance inside K0 to the other instances inside K0, and calculate the average distance from each instance inside K0 to the instances inside K3.
|
Instance |
Average Distance Inside K0 |
Average Distance Inside K3 |
Net Distance |
|
2 |
0.55 |
0.81 |
-0.26 |
|
3 |
0.55 |
0.83 |
-0.28 |
Step 25: Instance 3 has the greatest net distance, but …
Step 26: -0.28 < 0, so continue at Step 29.
Step 29: All net distances are < 0, so continue at Step 4.
Step 4: |K0| > 1 and |K1| > 1, so continue.
Step 5: Determine the diameter of each cluster containing more than one instance.
Step 6: The diameter of K0 and K1 is 0.55 and 0.80, respectively. Use K1 because it is largest.
Step 7: Increment a.
Step 8: Since |K1| > 2, go to Step 14.
Steps 14 and 15: K4 = {} and K = K ∪ K4. Thus,
K = {{2, 3}, {1, 4, 5}, {7}, {6}, {}}.
Step 16: Calculate the average distance between all pairs of instances in K1.
|
Instance |
Average Distance to Other Instances |
|
1 |
(0.33 + 0.66) / 2 = 0.50 |
|
4 |
(0.33 + 0.80) / 2 = 0.57 |
|
5 |
(0.66 + 0.80) / 2 = 0.73 |
Step 17: Instance 5 has the greatest average distance (i.e., it is least similar to the other instances).
Steps 18 and 19: K4 = K4 ∪ 5 and K1 = K1 − 5. Thus,
K = {{2, 3}, {1, 4}, {7}, {6}, {5}}.
Steps 21 to 24: Calculate the average distance from each instance inside K1 to the other instances inside K1, and calculate the average distance from each instance inside K1 to the instances inside K4.
|
Instance |
Average Distance Inside K1 |
Average Distance Inside K4 |
Net Distance |
|
1 |
0.33 |
0.66 |
-0.33 |
|
4 |
0.33 |
0.80 |
-0.47 |
Step 25: Instance 4 has the greatest net distance, but …
Step 26: -0.47 < 0, so continue at Step 29.
Step 29: All net distances are < 0, so continue at Step 4.
Step 4: |K0| > 1 and |K1| > 1, so continue.
Step 5: Determine the diameter of each cluster containing more than one instance.
Step 6: The diameter of K0 and K1 is 0.55 and 0.33, respectively. Use K0 because it is largest.
Step 7: Increment a.
Steps 8 and 9: |K0| = 2, so arbitrarily select instance 2 from K0.
Steps 10 to 12: K5 = {2}, K = K ∪ K5, and K0 = K0 − 2. Thus,
K = {{3}, {1, 4}, {7}, {6}, {5}, {2}}
and continue at Step 4.
Step 4: |K1| > 1, so continue.
Step 5: Determine the diameter of each cluster containing more than one instance. However, at this point, there is only one cluster, namely, K1, so…
Step 6: Use K1.
Step 7: Increment a.
Steps 8 and 9: |K1| = 2, so arbitrarily select instance 1 from K1.
Steps 10 to 12: K6 = {1}, K = K ∪ K6, and K1 = K1 − 1. Thus,
K = {{3}, {4}, {7}, {6}, {5}, {2}, {1}}
and continue at Step 4.
Step 4: There are no more clusters containing more than one instance, so done.
Single Link and Double Link Clusters
The distance function in this algorithm can determine similarity of clusters through many methods, including single link and group-average. Single link calculates the distance between two clusters as the shortest distance between any two objects contained in those clusters. Group-average first finds the average values for all objects in the group (i.e., cluster) and the calculates the distance between clusters as the distance between the average values.
Each object in D is initially used to create a cluster containing a single object. These clusters are successively merged into new clusters, which are added to the set of clusters, K. When a pair of clusters is merged, the original clusters are removed from K. Thus, the number of clusters in K decreases until there is only one cluster remaining, containing all the objects from D. The hierarchy of clusters is implicitly represented in the nested sets of K.