Notes 06-6: Terminology

For numeric attributes, clusters can be described by several characteristic values. Assume a cluster K_b consisting of n m-dimensional points .

The centroid, C_a, of a cluster K_a is the “middle” point of the cluster (it need not be an actual point in the cluster) and is described by  , where p_u, the u-th attribute of the centroid, is given by

The radius, R_a, of a cluster K_a is the square root of the average mean squared distance from all points in the cluster to the centroid, and is given by

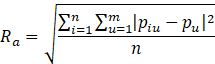
The diameter, Diameter_a, of cluster K_a is the square root of the average mean squared distance between all pairs of points in the cluster, and is given by

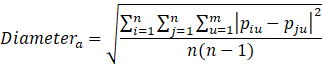
Many clustering algorithms require that the distance between clusters be determined (as opposed to the distance between objects) to identify when two clusters are of sufficient similarity to be linked together (i.e., amalgamated).

The single linkage (or nearest neighbor) method links clusters when the distance between the two closest objects in the different clusters is below some threshold.

The complete linkage (or furthest neighbor) method links clusters when the distance between the two furthest objects in the different clusters is below some threshold.

The pair-group average method links clusters when the average distance between all pairs of objects in the different clusters is below some threshold.

The pair-group centroid method links clusters when the distance between centroids is below some threshold.

The pair-group medoid method links clusters when the distance between medoids is below some threshold.