References:
S. Brin, R. Motwani, J.D. Ullman, S. Tsur, "Dynamic Itemset Counting and Implication Rules for Market Basket Data", SIGMOD Record, Volume 6, Number 2: New York, June 1997, pp. 255 - 264.
Su, Yibin, Dynamic Itemset Counting and Implication Rules for Market Basket Data: Project Final Report, CS831, April 2000.
Introduction
- Alternative to Apriori Itemset Generation
- Itemsets are dynamically added and deleted as transactions are read
- Relies on the fact that for an itemset to be frequent, all of its subsets must also be frequent, so we only examine those itemsets whose subsets are all frequent
Algorithm stops after every M transactions to add more itemsets.
- Train analogy: There are stations every M transactions. The passengers are itemsets. Itemsets can get on at any stop as long as they get off at the same stop in the next pass around the database. Only itemsets on the train are counted when they occur in transactions. At the very beginning we can start counting 1-itemsets, at the first station we can start counting some of the 2-itemsets. At the second station we can start counting 3-itemsets as well as any more 2-itemsets that can be counted and so on.
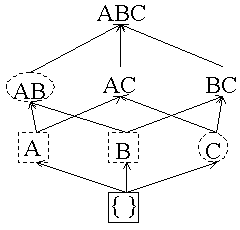
Itemsets are marked in four different ways as they are counted:
- Solid box:
confirmed frequent itemset - an itemset we have finished counting and exceeds the
support threshold minsupp - Solid circle:
confirmed infrequent itemset - we have finished counting and it is below
minsupp - Dashed box:
suspected frequent itemset - an itemset we are still counting that exceeds minsupp - Dashed circle:
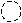suspected infrequent itemset - an itemset we are still counting that is
below minsupp
DIC Algorithm
A Java applet which combines DIC, Apriori and Probability Based Objected Interestingness Measures can be found here.
Algorithm:
- Mark the empty itemset with a solid square. Mark all the 1-itemsets with dashed circles. Leave all other itemsets unmarked.
- While any dashed itemsets remain:
- Read M transactions (if we reach the end of the transaction file, continue from the beginning). For each transaction, increment the respective counters for the itemsets that appear in the transaction and are marked with dashes.
- If a dashed circle's count exceeds minsupp, turn it into a dashed square. If any immediate superset of it has all of its subsets as solid or dashed squares, add a new counter for it and make it a dashed circle.
- Once a dashed itemset has been counted through all the transactions, make it solid and stop counting it.
Itemset lattices: An itemset lattice contains all of the possible itemsets for a transaction database. Each itemset in the lattice points to all of its supersets. When represented graphically, a itemset lattice can help us to understand the concepts behind the DIC algorithm.
- Example: minsupp = 25% and M = 2.
| TID | A | B | C |
| T1 | 1 | 1 | 0 |
| T2 | 1 | 0 | 0 |
| T3 | 0 | 1 | 1 |
| T4 | 0 | 0 | 0 |
Transaction Database
Itemset lattice for the above transaction database:
|
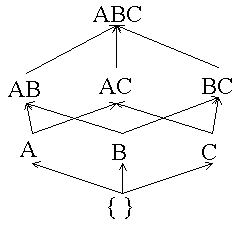
Itemset lattice before any transactions are read:
Counters: A = 0, B = 0, C = 0 Empty itemset is marked with a solid box. All 1-itemsets are marked with dashed circles. |
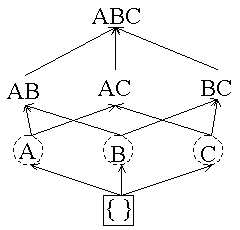
After M transactions are read:
Counters: A = 2, B = 1, C = 0, AB = 0 We change A and B to dashed boxes because their counters are greater than minsup (1) and add a counter for AB because both of its subsets are boxes. |
After 2M transactions are read:
Counters: A = 2, B = 2, C = 1, AB = 0, AC = 0, BC = 0 C changes to a square because its counter is greater than minsup.A, B and C have been counted all the way through so we stop counting them and make their boxes solid. Add counters for AC and BC because their subsets are all boxes. |
After 3M transactions read:
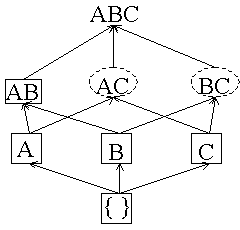
Counters: A = 2, B = 2, C = 1, AB = 1, AC = 0, BC = 0 AB has been counted all the way through and its counter satisfies minsup so we change it to a solid box. BC changes to a dashed box. |
After 4M transactions read:
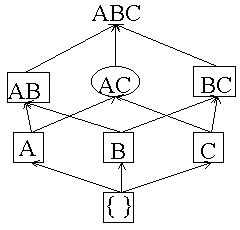
Counters: A = 2, B = 2, C = 1, AB = 1, AC = 0, BC = 1 AC and BC are counted all the way through. We do not count ABC because one of its subsets is a circle. There are no dashed itemsets left so the algorithm is done. |
Implementation
Go to the DIC Implementation page to see a working implementation in Java.
Operations:
- add new itemsets
- maintain a counter for every itemset
- manage itemset states from dashed to solid and from circle to square
- when itemsets become large determine which new itemsets should be added because they could potentially be large
Pseudocode Algorithm:
SS = Æ // solid square (frequent)
SC = Æ // solid circle (infrequent)
DS = Æ // dashed square (suspected frequent)
DC = { all 1-itemsets } // dashed circle (suspected infrequent)
while (DS != 0) or (DC != 0) do begin
SC = Æ // solid circle (infrequent)
DS = Æ // dashed square (suspected frequent)
DC = { all 1-itemsets } // dashed circle (suspected infrequent)
while (DS != 0) or (DC != 0) do begin
read M transactions from database into T
forall transactions t ÎTdo begin
forall transactions t ÎTdo begin
//increment the respective counters of the itemsets marked with dash
for each itemset c in DS or DC do begin
for each itemset c in DS
end
for each itemset c in DS or DC do begin
if ( c Î t ) then
for each itemset c in DC
c.counter++ ;
if ( c.counter ³ threshold ) then
end
move c from DC to DS ;
if ( any immediate superset sc of c has all of its subsets in SS or DS ) then
if ( any immediate superset sc of c has all of its subsets in SS or DS ) then
add a new itemset sc in DC ;
for each itemset c in DS
if ( c has been counted through all transactions ) then
for each itemset c in DC
move it into SS ;
if ( c has been counted through all transactions ) then
end
move it into SC ;
Answer = { c Î SS } ;