Reference:

• Hilderman, R.J., and Hamilton, H.J. ``Principles for Mining Summaries Using Objective Measures of Interestingness.'' In IEEE International Conference on Tools with Artificial Intelligence (ICTAI-2000) , Vancouver, BC, IEEE, November, 2000, pp. 72-81.
• Hilderman, R.J., and Hamilton, H.J. ``Measuring the Interestingness of Discovered Knowledge: A Principled Approach,'' Intelligent Data Analysis, 7(4), 2003. Accepted December, 2002.
• Barber, B., and Hamilton, H.J. ``Parametric Algorithms for Mining Share Frequent Itemsets,'' Journal of Intelligent Information Systems, 16(3):277-293, August, 2001.

Introduction

The share measure has been proposed (Carter et al., 1997) as an alternative measure of the importance of itemsets. In informal terms, share is the percentage of a numerical total that is contributed by the items in an itemset. In this section, we provide a formal description of the share measure. We start with a definition of the source of the numerical information, a measure attribute.

TID	Item A	Item B	Item C	Item D
T1	1	0	1	14
T2	0	0	6	0
T3	1	0	2	4
T4	0	0	4	0
T5	0	0	3	1
T6	0	0	1	13
T7	0	0	8	0
T8	4	0	0	7
T9	0	1	1	10
T10	0	0	0	18

Table 1: Sample Database

Definition 1. A measure attribute (MA) is a numerical attribute associated with each item in each transaction.

A numerical attribute can have an integer type, such as quantity sold, or a real type such as profit margin, unit cost, or total revenue.

Definition 2. The transaction measure value, denoted as tmv(I_p,T_q), is the value of a measure attribute associated with an item I_p in a transaction T_q.

The quantity sold values in Table 1 are the transaction measure values of the items in each transaction. For example, tmv(D,T1) = 14.

Definition 3. The global measure value of an item I_p, denoted as MV(I_p), is the sum of the transaction measure values of I_p in every transaction in which I_p appears, where

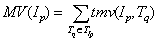
[1]

Using the sample data, MV(A) = tmv(A,T1) + tmv(A,T2) + tmv(A,T3) + tmv(A,T4) + tmv(A,T5) + tmv(A,T6) + tmv(A,T7) + tmv(A,T8) + tmv(A,T9) + tmv(A,T10) = 1 + 0 + 1 + 0 + 0 + 0 + 0 + 4 + 0 + 0 = 6. Similarly, MV(B) = 1, MV(C) = 26 and MV(D) = 67.

Definition 4. The total measure value (MV) is the sum of the global measure values for all items in I in every transaction in D, where

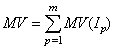
[2]

The total measure value provides a stable baseline, similar to the total number of transactions used in the support measure. In the sample database, MV = MV(A) + MV(B) + MV(C) + MV(D) = 6 + 1 + 26 + 67 = 100.

Definition 5. A k-itemset is an itemset X = {x₁, x₂, ..., x_k}, X ÍI, 1 £ k £m, of k distinct items. Each itemset X has an associated set of transactions T_X = {T_q ÎT | T_q Ê X}, which is the set of transactions that contain the itemset X.

Definition 6. The local measure value of an item x_i in an itemset X , denoted as lmv(x_i,X), is the sum of the transaction measure values of the item x_i in all transactions containing X, where

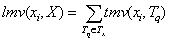
[3]

The local measure value for an item x_i will always be less than or equal to the global measure value for the item x_i, since the global measure value represents the sum of transaction measure values of item x_i in every transaction in which item x_i individually occurs, whether or not the complete itemset occurs in each of these transactions. A single item will have a separate local measure value for each itemset in which the item appears. Thus, the local measure value of some item I_p in the itemset X will be different from the local measure value of I_p in the itemset Z, if Z is not equal to X.

Definition 7. The local measure value of an itemset X, denoted as lmv(X), is the sum of the local measure values of each item in X in all transactions containing X, where

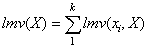
[4]

Definition 8. The item share of an item x_i in itemset X, denoted as SH(x_i,X), is the ratio of the local measure value of x_i in X to the total measure value, where

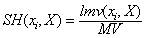
[5]

Definition 9. The itemset share of itemset X, denoted as share(X), is the ratio of the local measure value of X to the total measure value, where

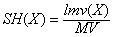
[6]

Based on the sample transaction database provided in Table 1, values corresponding to the measures described in Definitions 6, 7, 8 and 9 are provided in Table 2. The left-hand column lists all possible itemsets. The two columns under each item label show the local measure value and item share of the item in each of the itemsets in the left-hand column. For example, lmv(A,ACD) = 2 and recalling that MV = 100, SH(A, ACD) = lmv(A,ACD)/MV = 2/100 = 0.02. The two columns under the label Itemset X are the local measure value and itemset share of the itemsets in the left-hand column. For itemset ACD, lmv(ACD) = lmv(A, ACD) + lmv(C, ACD) + lmv(D, ACD) = 2 + 3 + 18 = 23 and SH(ACD) = lmv(ACD)/MV = 23/100 = 0.23. A dash in a table cell indicates that the itemset does not contain the item.

	Item A	Item B	Item C	Item D	Itemset X
Itemset	lmv	SH	lmv	SH	Lmv	SH	lmv	SH	lmv	SH
A	6	0.06	-	-	-	-	-	-	6	0.06
B	-	-	1	0.01	-	-	-	-	1	0.01
C	-	-	-	-	26	0.26	-	-	26	0.26
D	-	-	-	-	-	-	67	0.67	67	0.67
AB	-	-	-	-	-	-	-	-	0	0.00
AC	2	0.02	-	-	3	0.03	-	-	5	0.05
AD	6	0.06	-	-	-	-	25	0.25	31	0.31
BC	-	-	1	0.01	1	0.01	-	-	2	0.02
BD	-	-	1	0.01	-	-	10	0.10	11	0.11
CD	-	-	-	-	8	0.08	42	0.42	50	0.50
ABC	-	-	-	-	-	-	-	-	0	0.00
ABD	-	-	-	-	-	-	-	-	0	0.00
ACD	2	0.02	-	-	3	0.03	18	0.18	23	0.23
BCD	-	-	1	0.01	1	0.01	10	0.10	12	0.12
ABCD	-	-	-	-	-	-	-		0	0.00

Table 2: Sample Database Summary

Using the share measure, the frequent itemsets are defined to be those whose share is greater than or equal to minshare, a user specified threshold. If minshare = 0.2, then the frequent itemsets are those shown in bold face in Table 2. The association rules are created from the frequent itemsets in the same manner as with the support measure.