Convolutional Neural Networks
Convolution Filtering
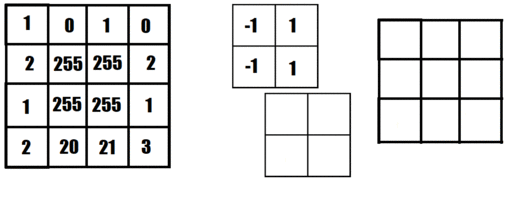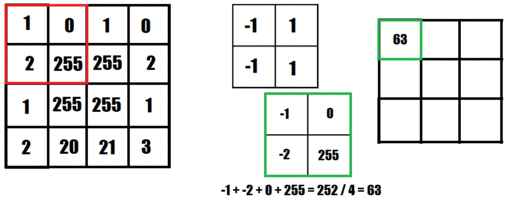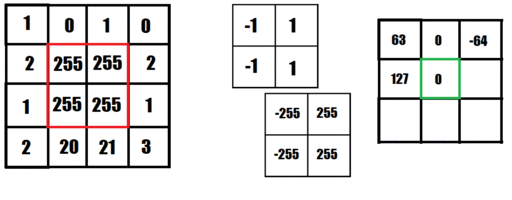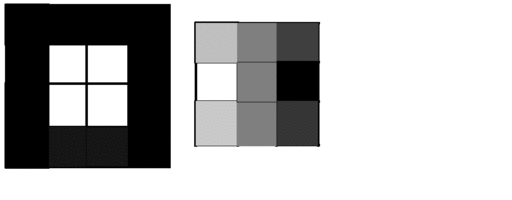
For years, convolutional filtering has been used to process and filter images. Convolutional filtering uses a kernel to sweep across an image to detect patterns in the image. A kernel is a very small matrix (usually 3x3 or 5x5) with a set of weights corresponding to its size. As the kernel sweeps across the image at each pixel, it combines the values of the pixels around that specific pixel multiplied by the respective weight in the kernel. The value from the kernel is then placed into a new image in the corresponding position.
The animation below shows an image being filtered to detect left-facing edges. The resulting image (to the right) then show positive values where left-facing edges are detected and negative values where right-facing edges are detected.
Pooling
Pooling in terms of Convolutional Neural Networks is a very important concept. An image, say 400x400, is far to big for small kernels to detect patterns, no matter how many filters you have. After convolution, it can be helpful to pool an image to a smaller size, usually cutting it in half. After pooling the 400x400 image would be 200x200.
There are two common methods of pooling. Average Pooling looks at groups of (typically four) pixels, then turns them into one pixel which contains the average of the respective pixels. Maximum Pooling looks at groups of (typically four) pixels, then turns them into one pixel which contains the maximum value of the respective pixels. Strides are taken according to the pool size. If the pool size is 2x2, the group of pixels will strides of two. This means the groups will not overlap, as the pooling filter is moved over by two pixels each iteration.
Another method of pooling which is not as common is to simply stride a convolutional kernel, jumping a few pixels each iteration.
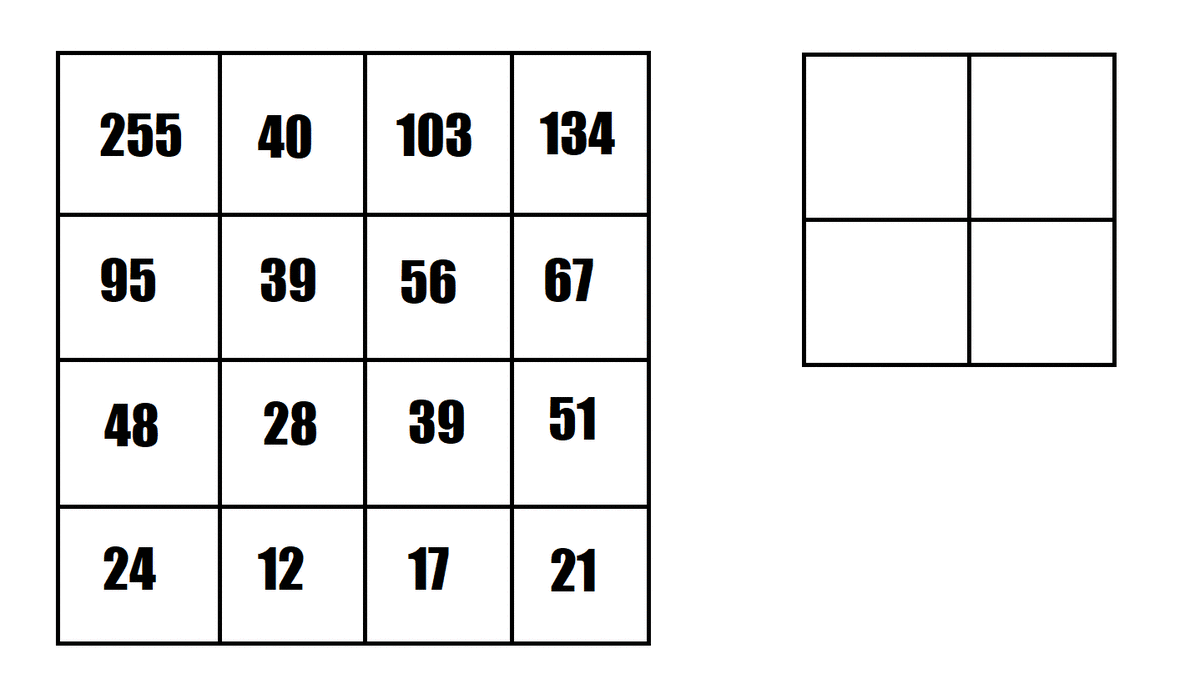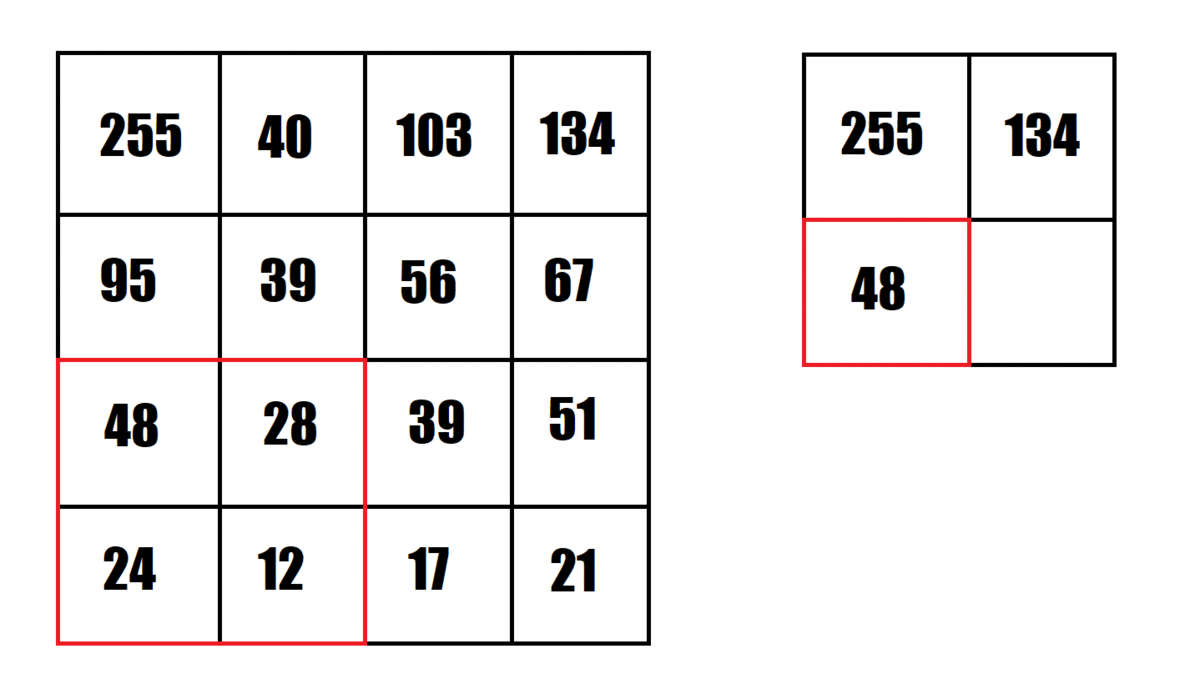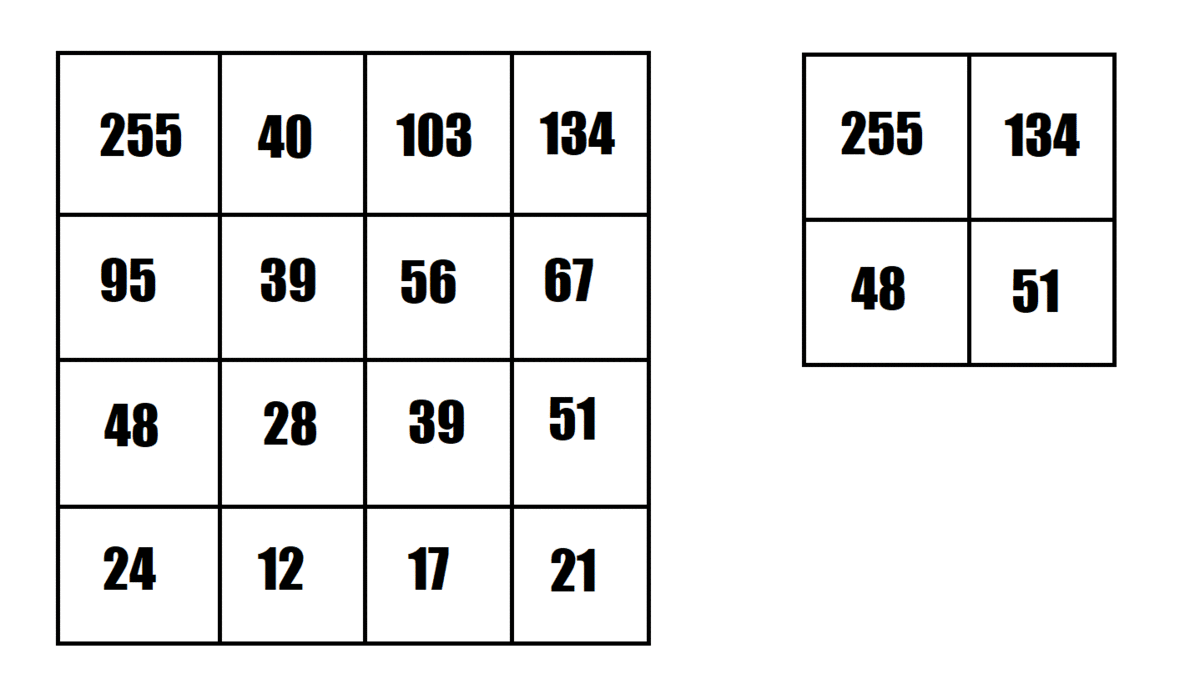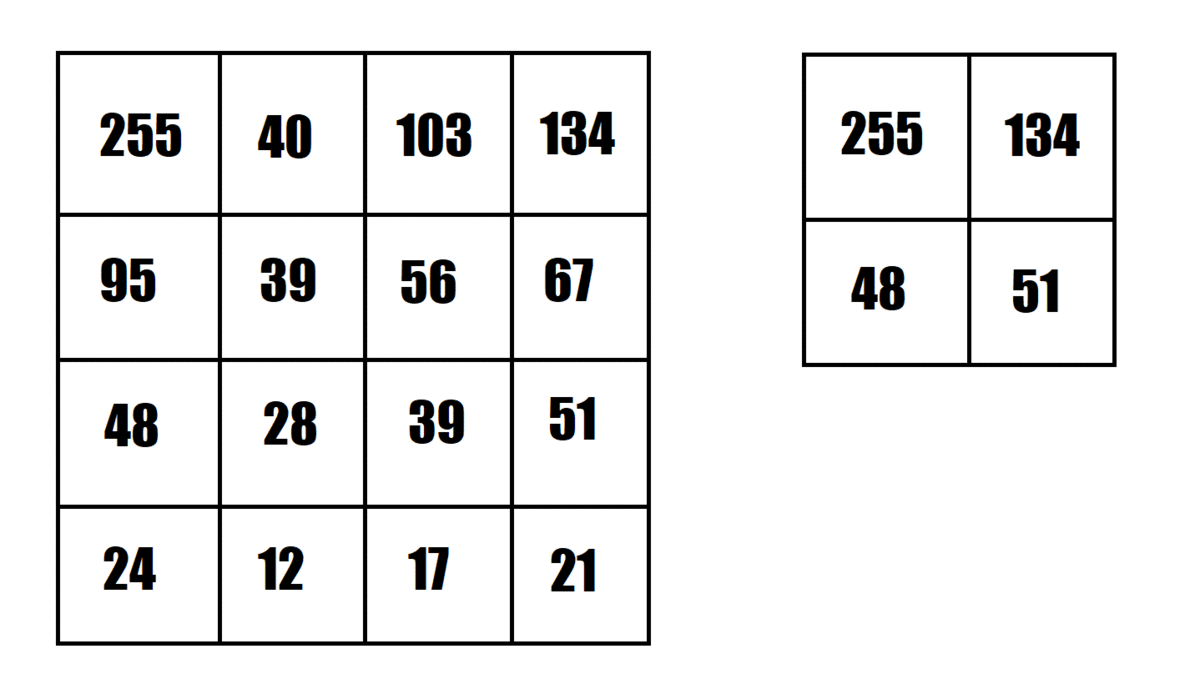
The animation provided shows an example of maximum pooling, using a 2x2 pooling filter and strides of 2. This shrinks the "image" from 4x4 to 2x2.
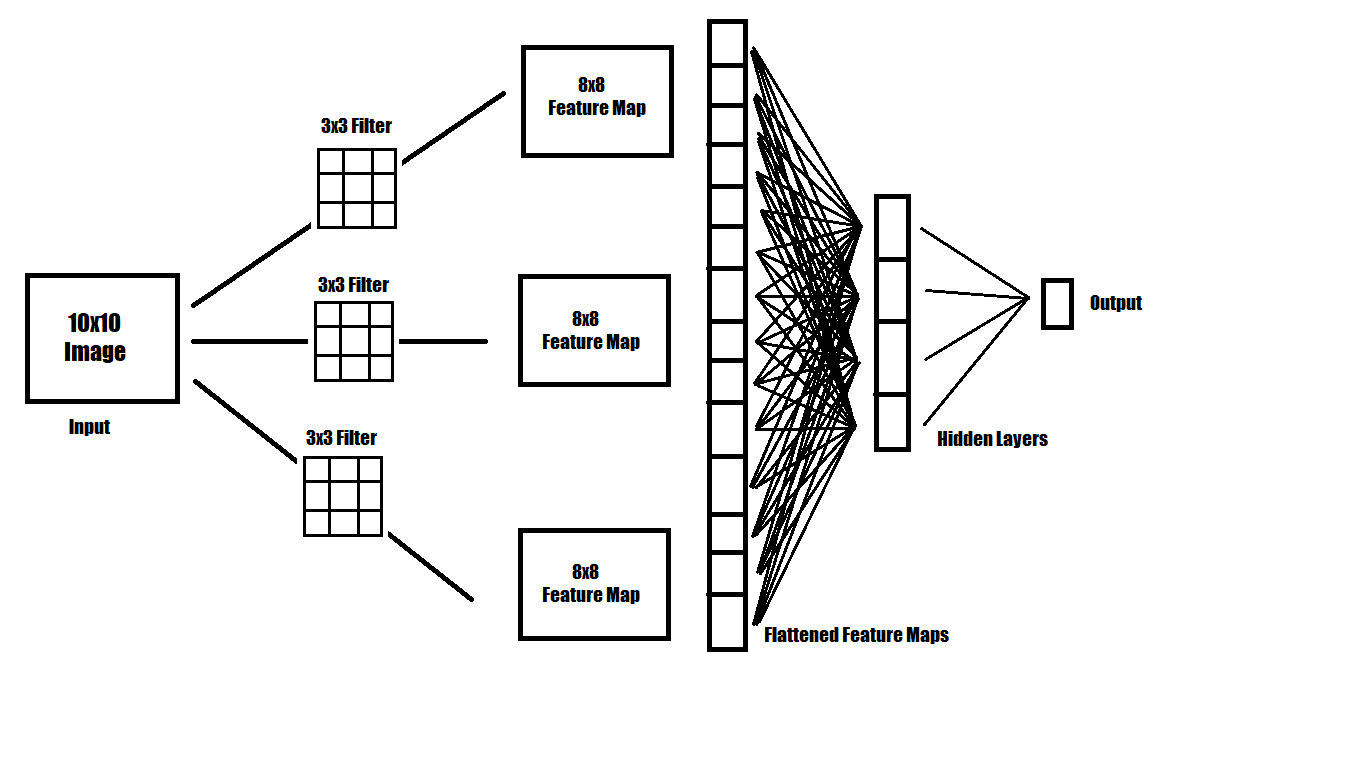
Shallow Convolutional Neural Network
When attempting to recognize patterns that are complex, more intuitive methods of filtering an image must be used. A simple neural network can be made that uses multiple filters on an image. After being filtered, multiple 'images' are derived, representing features of the original image. These are often called feature maps. Those feature maps can then be filtered further, or flattened into a 1 dimensional vector of values. From there, a small feed forward neural network can be used to translate those flattened feature vectors into classes.
The image provided shows an example of a simple convolutional neural network which gives one numerical output. In classification tasks, this output would be between 0 and 1, denoting the probability of whether the class exists in the image.