Introduction To Neural Networks
The Perceptron
A perceptron (also called a neuron), put simply, is just an element that takes an input, and given some parameters (usually a set of weights and a bias) outputs a new number.
The basic perceptron works as a simple linear function, with the slope being its weight, and y-intercept being its bias. This can be shown as function:
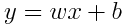
Where:
x is the input
y is the output
w is the weight
b is the bias
Each perceptron usually also includes a non-linearity (or activation function). This is an additional function calculated on the result of the above function. The most well-known activation function is the sigmoid function, defined as:
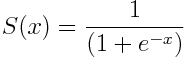

Where:
x is the output from the perceptron's weight, input and bias
S(x) is the output of the perceptron
Quite often, perceptrons receive more than one input. Each input is given its own weight value, multiplied with the value of that input. The sum of the weighted inputs is then calculated adding the bias on top. Finally, the activation function is applied.
The output of a perceptron can be represented through a function:
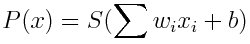
Where:
i denotes the index of the input
w is the corresponding weight
x is the corresponding input
b is the bias
S is the activation function
P(x) is the output
Multi-Layer Perceptron
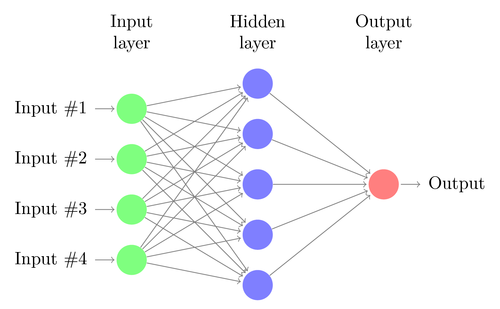
This image represents what is called a multi-layer perceptron, also called a neural network. The first layer represents a structure of inputs (also called features). These features are fed to the hidden layer perceptrons, and each of those values are calculated. The results of those hidden layer perceptrons are then fed to the output layer perceptrons.
Any number of hidden layers can be stacked with eachother, making a neural network more complex. Hidden layers can have any number of perceptrons, depending on how complex the task at hand is. Input and output layers have the number of perceptrons corrseponding to the task.
An example of where a multi-layer perceptron may be useful is in predicting whether a house will sell. An input vector containing values such as price, number of bedrooms, bathrooms, and square footage may be the input. The output would be a value between 0 and 1, denoting the probability that the house will sell.
Neural Networks can be used like this for logistic regression. Neural Networks can be used for any kind of regression, simply by changing the activation functions used inside.
Learning Methods
There are 3 common methods of teaching a multi-layer perceptron to perform its intended task:
Reinforcement Learning, Supervised Learning and Unsupervised Learning.
Reinforcement learning and supervised learning are far more significant than unsupervised learning.
Reinforcement Learning
Reinforcement learning teaches a neural network by rewarding it for working well and punishing it for not. This lesson will not go in-depth on any reinforcement learning methods, but the most common methods of reinforcement learning are Q-Learning and Genetic Algorithms. Reinforcement works best on tasks where there isn't a right and wrong answer, but rather answers that work better or worse given an environment. For example, reinforcement learning is used in neural networks that learn to play games.
Supervised Learning
Supervised Learning is used where there is a right and wrong answer. The neural network makes an attempt on an input, and is then given a cost value based on how far it was from the correct output. The network then traces its steps backwards and makes adjustments to its weights and biases, using a method called Backpropagation and Gradient Descent. Supervised learning works best on tasks such as prediction, regression and classification. For exampline, supervised learning is used in neural networks that classify images of hand-written numbers.
Gradient Descent
Cost Function
A cost function, which is a key component to a neural network's ability to learn, aims to denote how far a perceptron's prediction is from the correct prediction. The simplest loss function is the squared error function:
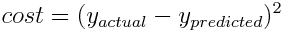
Climbing Hills In The Dark
Imagine you want to climb to the top of a hill, but there's a solar eclipse in effect. You can't see a thing, but you know you want to get to the top of the hill. How will you manage to get to the top of the hill, only being able to feel the ground beneath you?
If you are standing beside the hill, the ground beneath you will have a slope, leading upwards in some direction. You take a step in whichever direction leads you to a higher elevation. You feel the ground again and find which direction leads you higher. Eventually, after a few hundred steps, you reach the top of the hill, where every direction you could possibly step leads to a lower elevation, and your task is complete.
Minimizing Cost
Imagine a network in which you have 1 input, 1 output, and no hidden layers. The average cost on a set of parameters would be a 3 dimensional function, where the first dimension is based on the networks single weight parameter, the second dimension is the networks single bias parameter, and the third dimension is the average cost of the predictions given those two parameters.
The graphed function, for example, may look like this:
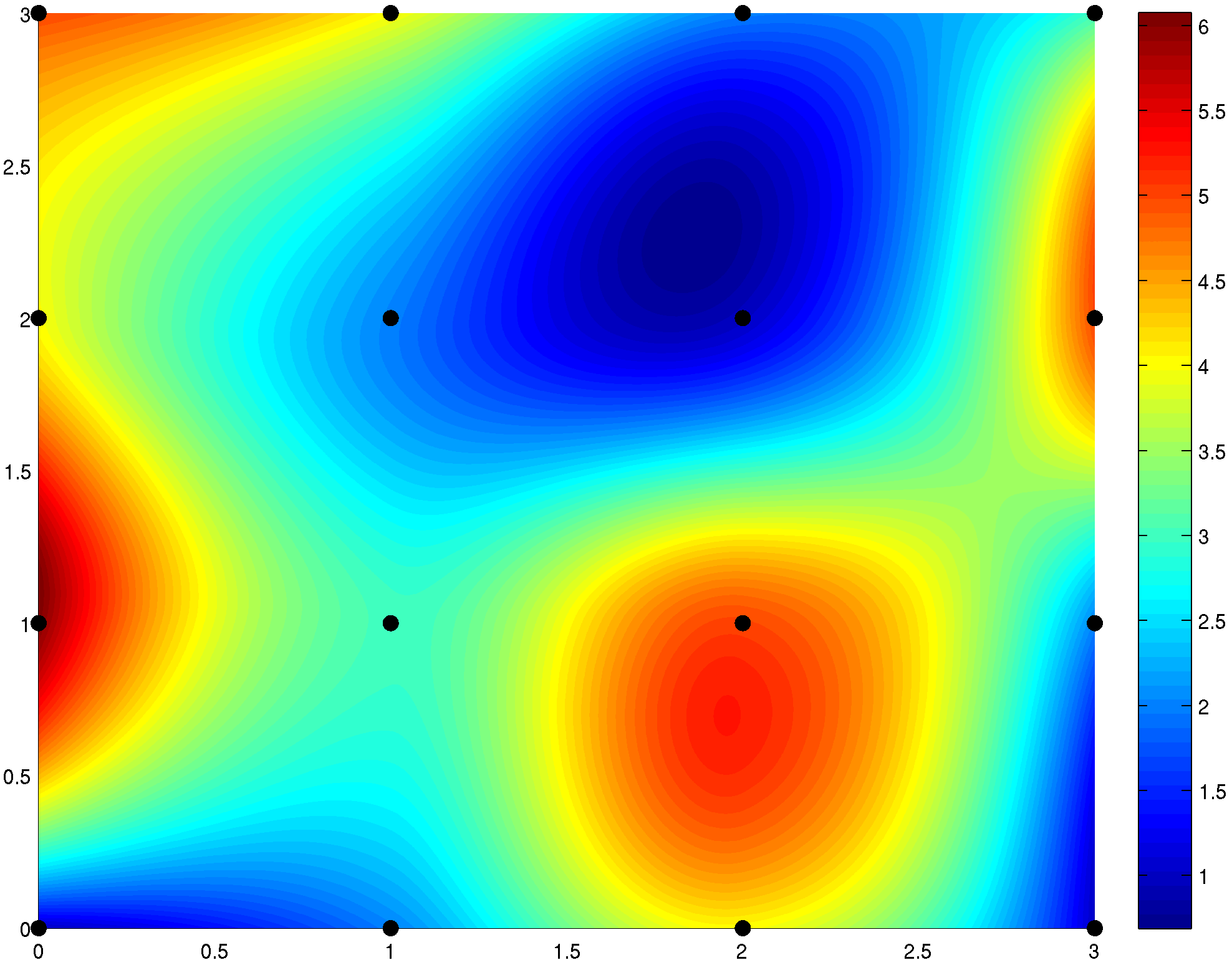
The network would be initialized at some random point on that function, and would aim to get to the lowest (blue) point. This would mean minimizing the cost function, which would imply that the network is close to being accurate.
Just like in the hill-climbing illustration, one could find the direction that has the most downward slope, and take a step in that direction. Taking that step means to adjust the parameters of the function - the 1 weight and 1 bias. Here is an example of gradient descent steps:
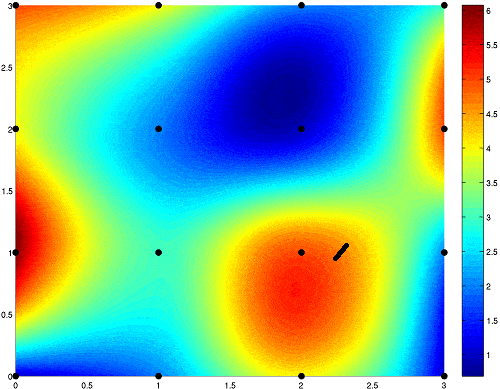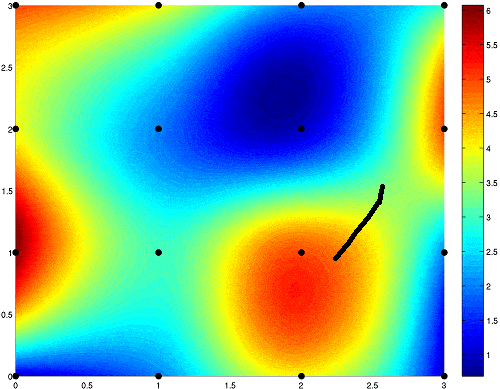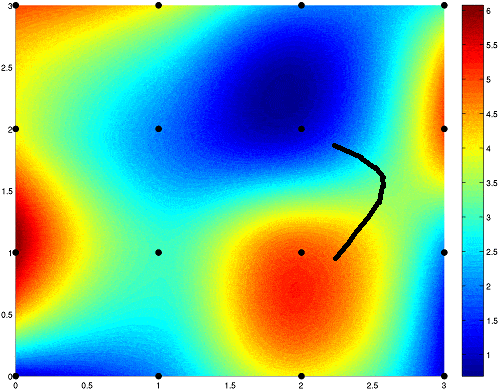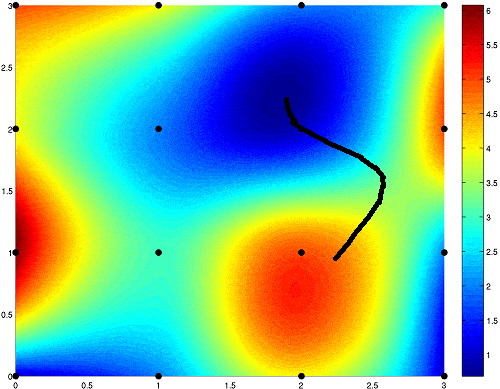
This works the exact same way with larger networks, but is much more difficult as a network with more weights and biases would have more than 3 dimensions. In supervised learning, the desired direction is computed using a method called backpropagation.
Additional Resources
Video Playlist on Neural Networks
This playlist is an easy to understand explanation on the basics of neural networks, taught in this lesson. The videos are made by 3Blue1Brown and work through making a neural network that classifies hand-written digits. The videos touch on perceptrons, multi-layer perceptrons, loss functions, backpropagation and the math behind it all.
This playlist is an easy to understand explanation on the basics of neural networks, taught in this lesson. The videos are made by 3Blue1Brown and work through making a neural network that classifies hand-written digits. The videos touch on perceptrons, multi-layer perceptrons, loss functions, backpropagation and the math behind it all.