

Next:PostfixInfix
and Prefix Up:Assignment
2Previous:Assignment
2
The polynomial ADT(12 points)
Implementation of the ADT polynomial(9
points)
Given the polynomial ADT(see below), write the routines required to perform
the different operations in the two following cases:
-
An array is used to store the different coefficients of the polynomial.
The size of the array is equal the degree+1 where degree
is the degree of the polynomial, e.g. :
-
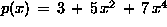
-
Array representation:

-
A singly linked list is used to store the different terms of the polynomial:
pairs
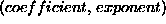 representing the non negative coefficients and their corresponding exponent,
e.g. the singly linked list representation of the example above is:
representing the non negative coefficients and their corresponding exponent,
e.g. the singly linked list representation of the example above is:

Structure Polynomial is
Data: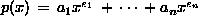 : a set of sorted pairs
: a set of sorted pairs 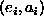 .
.
Functions:
for every poly, poly1, poly2 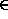 Polynomial, coef
Polynomial, coef 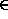 Coefficient, expon
Coefficient, expon 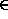 Exponents
Exponents
Polynomial Zero() ::= return the
polynomial p(x)=0
Boolean isZero(poly) ::= return
(poly == 0)
Coefficient Coeff(poly , expon) ::=
If
(expon 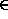 poly) return its corresponding coefficient else return 0
poly) return its corresponding coefficient else return 0
Exponent LeadExp(poly) ::= return
the degree of poly
Polynomial Remove(poly , expon) ::=
If
(expon 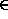 poly) remove the corresponding term and return the new poly
else return ERROR
poly) remove the corresponding term and return the new poly
else return ERROR
Polynomial SingleMult(poly , coef , expon)
::= return poly 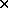 coef x
coef x 
Polynomial Add(poly1 , poly2) ::= return
poly1 + poly2
Polynomial Mult(poly1 , poly2) ::=
return
poly1 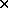 poly2
poly2
end Polynomial
Experimental study of the two
representations(3 points)
While time complexities of the different routines in the case of array
representation are comparable to those of linked list representation, for
non dense polynomials, where most terms of the polynomial are not present,
the running time of the multiplication is very slow and sometimes unacceptable
in the case of array representation.
Using the following parameter, compare the running time required by
the multiplication in both kind of representation:
Malek Mouhoub
Friday February 4 19:04:44 MST 2000
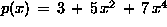
![]()
![]()
![]()
![]() Polynomial, coef
Polynomial, coef ![]() Coefficient, expon
Coefficient, expon ![]() Exponents
Exponents
![]() poly) return its corresponding coefficient else return 0
poly) return its corresponding coefficient else return 0
![]() poly) remove the corresponding term and return the new poly
else return ERROR
poly) remove the corresponding term and return the new poly
else return ERROR
![]() coef x
coef x ![]()
![]() poly2
poly2
![]()