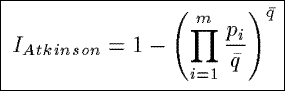Please Reference the Following Paper:

• Hilderman, R.J., and Hamilton, H.J. ``Heuristic Measures of Interestingness.'' In Third European Symposium on Principles of Data Mining and Knowledge Discovery (PKDD'99), Prague, Czech Republic, Springer Verlag, September, 1999, 232-241.

Introduction

The sixteen measurses that make up the HMI set come from the areas of economics, ecology, and information theory. Collectively, we refer to these sixteen measures as the HMI set (i.e., heuristic measures of interestingness).

The measures can be used for more than just ranking the interestingness of generalized relations using domain generaliztion graph. For example, alternative methods could be used to guide the generation of summaries, such as Galois lattices, conceptual graphs, or formal concept analysis. Also, summarties could more generally include views generated from databases or summary tables generated from data cubes.

Sixteen Characteristics of the HMI Set

Each measure shares three important properties

• Depends only on the frequency distribution or probability distribution of the values in the derived Count attribute of the summary to which it is being applied.
• Allows a value to be generated with at most one pass through the summary.
• Is independent of any specific units of measure.

Variables used in describing of the HMI set

• Let m be the total number of tuples in a summary
• Let n_i be the value contained in the Count attribute for tuple t_i
• Let N be the total count
• Let p be the observed probability (i.e. relative frequency) distribution of the tuples Based on the values n_i
• Let p_i = n_i / N be the observed probability for tuple t_i
• Let q be a uniform probability distribution of the tuples
• Let u = N / m be the count for tuple t_i, i = 1,2,...,m according to the uniform distribution q
• Let q-bar = 1 / m be the probability for tuple t_i, i = 1,2,...,m according to the uniform distribution q
• Let r be the probability distribution obtained by combining the values n_i and u
• Let r_i = (n_i + u) / 2N, be the probability for tuples t_i, for all i = 1,2,...,m according to distribution r

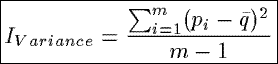
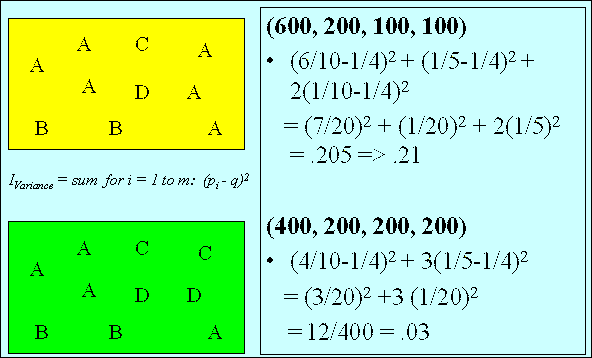
I_Variance
Based on the sample variance from classical statistics, I_Variance measures the weighted average of the squared deviations of the probabilities p_i from the mean probability q-bar, where the weight assigned to each squared deviation is 1/(m - 1).

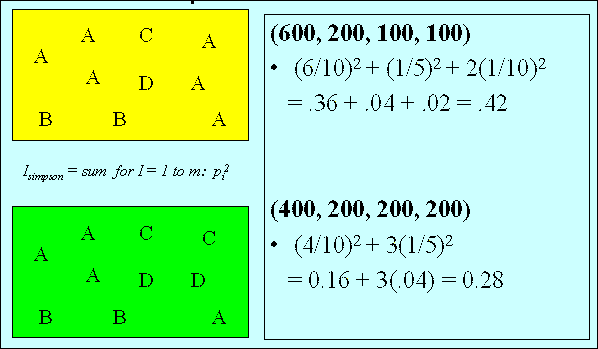
I_Simpson
A variance-like measure based on the Simpson index, I_Simpson measures the extent to which the counts are distributed over the tuples in a summary, rather than being concentrated in any single one of them.

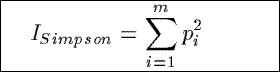
I_Shannon
Based on a relative entropy measure from information theory (known as the Shannon index), I_Shannon measures the average information content in the tuples of a summary.

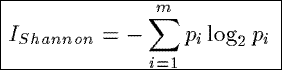
I_Total
Based on the Shannon index from information theory, I_Total measures the total information content in a summary.

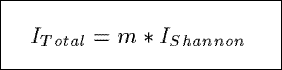
I_Max
Based on the Shannon index from information theory, I_Max measures the maximum possible information content in a summary.

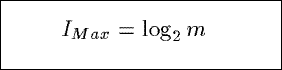
I_McIntosh
Based on a heterongeneity index from ecology, I_McIntosh views the counts in a summary as the coordinates of a point in a multidimensional space and measures the modified Euclidean distance from this point to the origin.

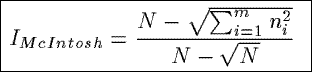
I_Lorenz
Based on the Lorenz curve from statistics, economics, and social science, I_Lorenz measures the average value of the Lorenz curve derived from the probabilities p_i associated with the tuples in a summary. The Lorenz curve is a series of straight lines in a square of unit length, starting from the origin and going successively to points (p₁,q₁),(p₁ + p₂, q₁ + q₂), . . .. When the p_i's are all equal, the Lorenz curve coincides with the diagonal that cuts the unit square into equal halves. When the p_i's are not all equal, the Lorenz curve is below the diagonal.

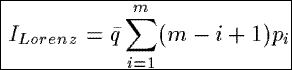
I_Gini
Based on the Gini coefficient which is defined in terms of the Lorenz curve, I_Gini measures the ratio of the area between the diagonal (i.e., the line of equality) and Lorenz curve, and the total area below the diagonal.

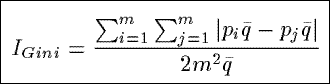
I_Berger
Based on a dominance index from ecology, I_Berger measures the proportional dominance of the tuple in a summary with the highest probability p_i

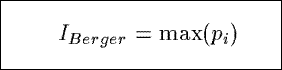
I_Schutz
Based on an inequality measure from the economics and social science, I_Schutz measures the relative mean deviation of the observed distribution of the counts in a summary from a uniform distribution of the counts.

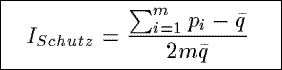
I_Bray
Based on a community similarity index from the ecology, I_Bray measures the percentage of similarity between the observed distribution of the counts in a summary and a uniform distribution of the counts.

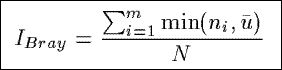
I_Whittaker
Based on a community similarity index from ecology, I_Whittaker measures the fraction of similarity between the observed distribution of the counts in a summary and a uniform distribution of the counts.

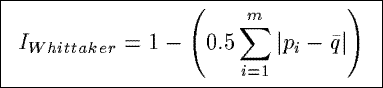
I_Kullback
Based on a distance measure from information theory, I_Kullback measures the distance between the observed distribution of the counts in a summary and a uniform distribution of the counts.

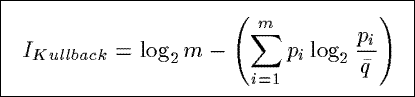
I_MacArthur
Based on the Shannon index from information theory, I_MacArthur combines two summaries, and then measures the difference between the amount of information contained in the combined distribution and the amount of contained in the average of the two original distributions.

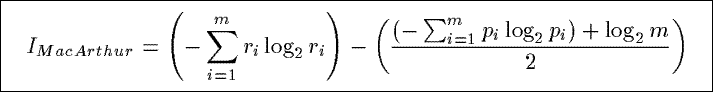
I_Theil
Based on a distance measure from the information theory, I_Theil measures the distance between the observed distribution of the counts in a summary and a uniform distribution of the counts.

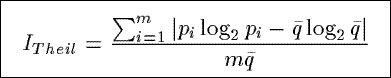
I_Atkinson
Based on a measure of inequality from economics, I_Atkinson measures the percentage to which the population in a summary would have to be increased to achieve the same level of interestingness as if the counts in the summary were uniformly distributed.