Reference:
- Geng, Liqiang and Hamilton, H.J. "Interestingness Measures for Data Mining: A Survey" In ACM Computing Surveys, 28(3).
- Information about other references can be found in the Interestingness Measures: A Selected Bibliography page
Introduction
A very important aspect of data mining research is the determination of how interesting a pattern is. Researchers have created 9 classifications for measures of interestingness.
Conciseness
A pattern is concise if it contains relatively few attribute-value pairs, while a set of patterns is concise if it contains relatively few patterns. A concise pattern or set of patterns is relatively easy to understand and remember and thus is added more easily to the userís knowledge (set of beliefs). Accordingly, much research has been conducted to find a ďminimum set of patterns,Ē using properties such as monotonicity [Padmanabhan and Tuzhilin 2000] and confidence invariance [Bastide et al. 2000].
Generality/Coverage
A pattern is general if it covers a relatively large subset of a dataset. Generality (or coverage) measures the comprehensiveness of a pattern, that is, the fraction of all records in the dataset that matches the pattern. If a pattern characterizes more information in the dataset, it tends to be more interesting [Agrawal and Srikant 1994; Webb and Brain 2002]. Frequent itemsets are the most studied general patterns in the data mining literature. An itemset is a set of items, such as some items from a grocery basket. An itemset is frequent if its support, the fraction of records in the dataset containing the itemset, is above a given threshold [Agrawal and Srikant 1994]. The best known algorithm for finding frequent itemsets is the Apriori algorithm [Agrawal and Srikant 1994]. Some generality measures can form the bases for pruning strategies; for example, the support measure is used in the Apriori algorithm as the basis for pruning itemsets. For classification rules, Webb and Brain [2002] gave an empirical evaluation showing how generality affects classification results. Generality frequently coincides with conciseness because concise patterns tend to have greater coverage.
Examples of Generatlity/Coverage association rules: support, coverage
Reliability
A pattern is reliable if the relationship described by the pattern occurs in a high percentage of applicable cases. For example, a classification rule is reliable if its predictions are highly accurate, and an association rule is reliable if it has high confidence. Many measures from probability, statistics, and information retrieval have been proposed to measure the reliability of association rules [Ohsaki et al. 2004; Tan et al. 2002].
Examples of Reliability association rules: confidence, added value, lift
Peculiarity
A pattern is peculiar if it is far away from other discovered patterns according to some distance measure. Peculiar patterns are generated from peculiar data (or outliers), which are relatively few in number and significantly different from the rest of the data [Knorr et al. 2000; Zhong et al. 2003]. Peculiar patterns may be unknown to the user, hence interesting.
Diversity
A pattern is diverse if its elements differ significantly from each other, while a set of patterns is diverse if the patterns in the set differ significantly from each other. Diversity is a common factor for measuring the interestingness of summaries [Hilderman and Hamilton 2001]. According to a simple point of view, a summary can be considered diverse if its probability distribution is far from the uniform distribution. A diverse summary may be interesting because in the absence of any relevant knowledge, a user commonly assumes that the uniform distribution will hold in a summary. According to this reasoning, the more diverse the summary is, the more interesting it is. We are unaware of any existing research on using diversity to measure the interestingness of classification or association rules.
Novelty
A pattern is novel to a person if he or she did not know it before and is not able to infer it from other known patterns. No known data mining system represents everything that a user knows, and thus, novelty cannot be measured explicitly with reference to the userís knowledge. Similarly, no known data mining system represents what the user does not know, and therefore, novelty cannot be measured explicitly with reference to the userís ignorance. Instead, novelty is detected by having the user either explicitly identify a pattern as novel [Sahar 1999] or notice that a pattern cannot be deduced from and does not contradict previously discovered patterns. In the latter case, the discovered patterns are being used as an approximation to the userís knowledge.
Surprisingness
A pattern is surprising (or unexpected) if it contradicts a personís existing knowledge or expectations [Liu et al. 1997, 1999; Silberschatz and Tuzhilin 1995, 1996]. A pattern that is an exception to a more general pattern which has already been discovered can also be considered surprising [Bay and Pazzani 1999; Carvalho and Freitas 2000]. Surprising patterns are interesting because they identify failings in previous knowledge and may suggest an aspect of the data that needs further study. The difference between surprisingness and novelty is that a novel pattern is new and not contradicted by any pattern already known to the user, while a surprising pattern contradicts the userís previous knowledge or expectations.
Utility
A pattern is of utility if its use by a person contributes to reaching a goal. Different people may have divergent goals concerning the knowledge that can be extracted from a dataset. For example, one person may be interested in finding all sales with high profit in a transaction dataset, while another may be interested in finding all transactions with large increases in gross sales. This kind of interestingness is based on user-defined utility functions in addition to the raw data [Chan et al. 2003; Lu et al. 2001; Yao et al. 2004; Yao and Hamilton 2006].
Actionability
A pattern is actionable (or applicable) in some domain if it enables decision making about future actions in this domain [Ling et al. 2002;Wang et al. 2002]. Actionability is sometimes associated with a pattern selection strategy. So far, no general method for measuring actionability has been devised. Existing measures depend on the applications. For example, Ling et al. [2002], measured actionability as the cost of changing the customerís current condition to match the objectives, whereas Wang et al. [2002], measured actionability as the profit that an association rule can bring.
Classifying Criteria
These nine criteria can be further categorized into three classifications: objective, subjective, and semantics-based. An objective measure is based only on the raw data. No knowledge about the user or application is required. Most objective measures are based on theories in probability, statistics, or information theory. Conciseness, generality, reliability, peculiarity, and diversity depend only on the data and patterns, and thus can be considered objective.
A subjective measure takes into account both the data and the user of these data. To define a subjective measure, access to the userís domain or background knowledge about the data is required. This access can be obtained by interacting with the user during the data mining process or by explicitly representing the userís knowledge or expectations. In the latter case, the key issue is the representation of the userís knowledge, which has been addressed by various frameworks and procedures for data mining [Liu et al. 1997, 1999; Silberschatz and Tuzhilin 1995, 1996; Sahar 1999]. Novelty and surprisingness depend on the user of the patterns, as well as the data and patterns themselves, and hence can be considered subjective.
A semantic measure considers the semantics and explanations of the patterns. Because semantic measures involve domain knowledge from the user, some researchers consider them a special type of subjective measure [Yao et al. 2006]. Utility and actionability depend on the semantics of the data, and thus can be considered semantic. Utility-based measures, where the relevant semantics are the utilities of the patterns in the domain, are the most common type of semantic measure. To use a utility-based approach, the user must specify additional knowledge about the domain. Unlike subjective measures, where the domain knowledge is about the data itself and is usually represented in a format similar to that of the discovered pattern, the domain knowledge required for semantic measures does not relate to the userís knowledge or expectations concerning the data. Instead, it represents a utility function that reflects the userís goals. This function should be optimized in the mined results. For example, a store manager might prefer association rules that relate to high-profit items over those with higher statistical significance.
An association rule is defined in the following way [Agrawal and Srikant 1994]: Let I = {i1, i2, . . . , im} be a set of items. Let D be a set of transactions, where each transaction T is a set of items such that T ? I . An association rule is an implication of the form X ? Y , where X ? I , Y ? I , and X n Y = f. The rule X ? Y holds for the dataset D with support s and confidence c if s% of transactions in D contain X ? Y and c% of transactions in D that contain X also contain Y . In this article, we assume that the support and confidence measures yield fractions from [0, 1], rather than percentages. The support and confidence measures were the original interestingness measures proposed for association rules [Agrawal and Srikant 1994].
Categories of Measures
ASSOCIATION RULES/CLASSIFICATION RULES:
- Objective Measures
- Based on probability (generality and reliability)
- Based on the form of the rules
- Peculiarity
- Surprisingness
- Conciseness
- Nonredundant rules
- Minimum description length
- Subjective Measures
- Surprisingness
- Novelty
- Semantic Measures
- Utility
- Actionability
SUMMARIES:
- Objective Measures
- Diversity of summaries
- Conciseness of summaries
- Peculiarity of cells in summaries
- Subjective Measures
- Surprisingness of summaries
Properties of Probability Based Objective Interestingness Measure
Piatetsky-Shapiro [1991] proposed three principles that should be obeyed by any objective measure, F:
- (P1) F = 0 if A and B are statistically independent, that is, P(AB) = P(A)P(B).
- (P2) F monotonically increases with P(AB) when P(A) and P(B) remain the same.
- (P3) F monotonically decreases with P(A) (or P(B)) when P(AB) and P(B) (or P(A)) remain the same.
Tan et al. [2002] proposed five properties based on operations for 2 ◊ 2 contingency tables.
- (O1) F should be symmetric under variable permutation.
- (O2) F should be the same when we scale any row or column by a positive factor.
- (O3) F should become ĖF if either the rows or the columns are permuted, that is, swapping either the rows or columns in the contingency table makes interestingness values change their signs.
- (O4) F should remain the same if both the rows and columns are permuted.
- (O5) F should have no relationship with the count of the records that do not contain A and B.
Lenca et al. [2004] proposed five properties to evaluate association measures
- (Q1) F is constant if there is no counterexample to the rule.
- (Q2) F decreases with P(A¨B) in a linear, concave, or convex fashion around 0+.
- (Q3) F increases as the total number of records increases.
- (Q4) The threshold is easy to fix.
- (Q5) The semantics of the measure are easy to express.
Analysis of Probability Based Objective Interestingness Measures
A Java applet which combines DIC, Apriori and Probability Based Objected Interestingness Measures can be found here.
.zip files containing the images and Latex files for all of the Probability Based Objective Interestingness Measures and the example calculations can be found at the end of this page
The interestingness measures will be analyzed using the second example database from the Apriori Itemset Generation page.
For clarity, the letters representing items have been changed to S, T, U, V, W (from A, B, C, D, E). The frequent itemset used for all of the interestingness measures is 'S T V' (or '1 2 4').
| TID | S | T | U | V | W |
| T1 | 1 | 1 | 1 | 0 | 0 |
| T2 | 1 | 1 | 1 | 1 | 1 |
| T3 | 1 | 0 | 1 | 1 | 0 |
| T4 | 1 | 0 | 1 | 1 | 1 |
| T5 | 1 | 1 | 1 | 1 | 0 |
A = 'V'
B = 'S T'
The provided reference for each interestingness measure may not be the true origin. If you know the origin, please contact us.
Support:
[Agrawal et al. 1996]
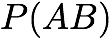
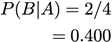
Confidence/Precision:
[Agrawal et al. 1996]
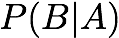
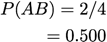
Coverage:
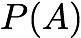
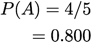
Prevalence:
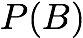
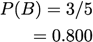
Recall:
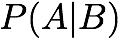
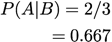
Specificity:
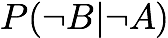
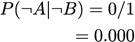
Accuracy:
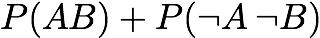
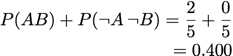
Lift/Interest:
[Brin et al. 1997]
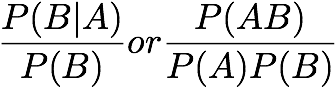
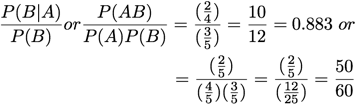
Leverage:
[Piatetsky-Shapiro 1991]
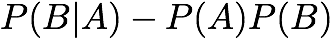
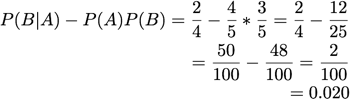
Added Value/Change of Support:
[Pavillon 1991]
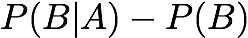
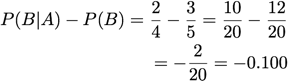
Relative Risk:
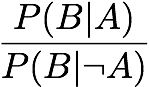
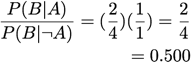
Jaccard:
[Tan et al. 2002]
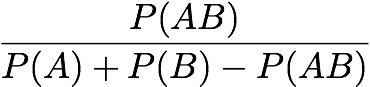
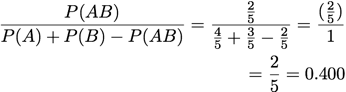
Certainty Factor:
[Tan & Kumar 2000]
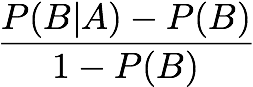
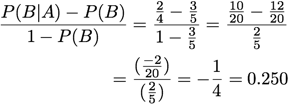
Odds Ratio:
[Tan & Kumar 2000]
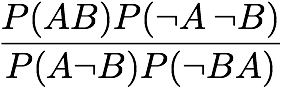
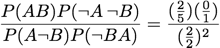
Yule's Q:
[Tan & Kumar 2000]
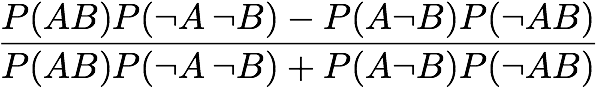
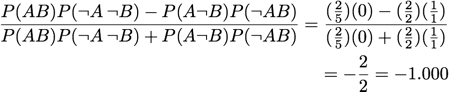
Yule's Y:
[Tan & Kumar 2000]
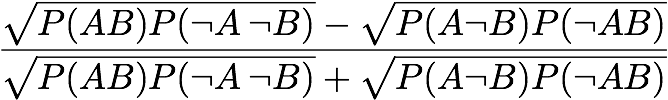
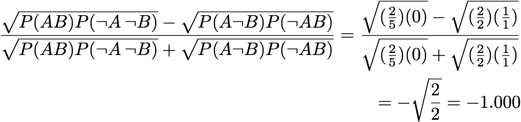
Klosgen:
[Klosgen 1996]
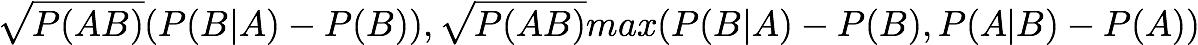
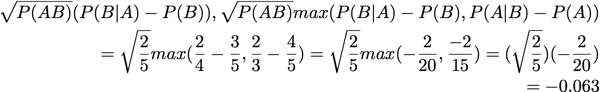
Conviction:
[Brin et al. 1997]
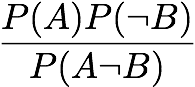
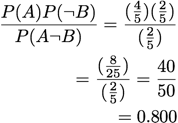
Interestingness Weighting Dependency:
[Gray and Orlowska 1998]
Assuming k and m value of 2
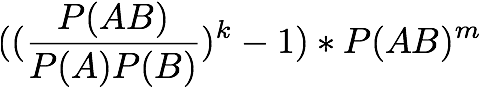
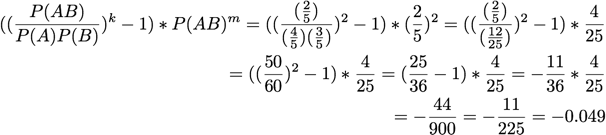
Collective Strength:
[Aggarwal & Yu 1998]
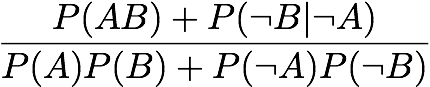
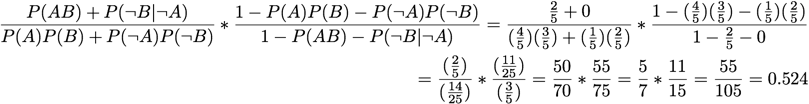
Laplace Correction:
[Tan & Kumar 2000]
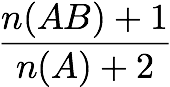
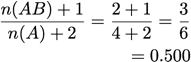
Gini Index:
[Tan et al., 2002]
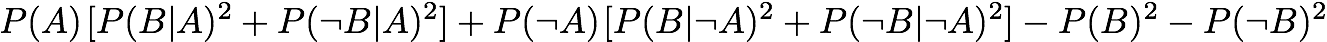
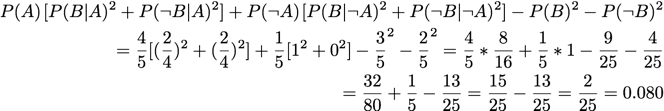
Goodman and Kruskal:
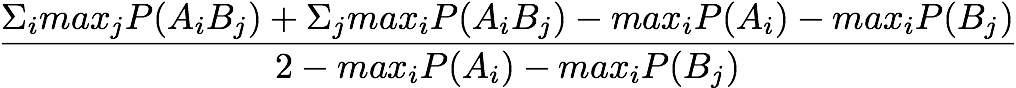
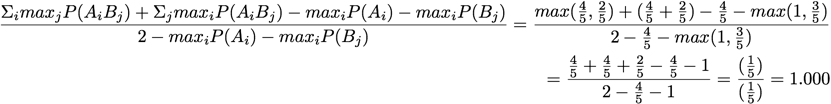
Normalized Mutual Information:
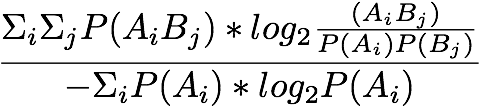
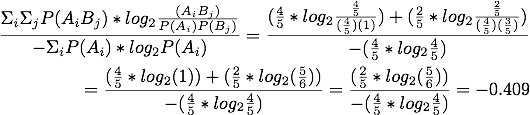
J-Measure:
[Goodman & Kruskal 1959]
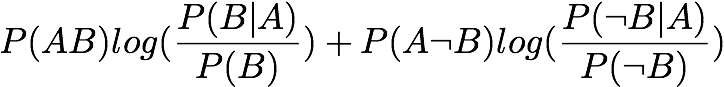
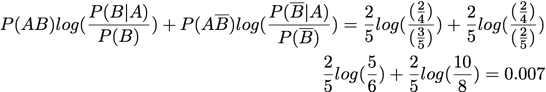
One-Way Support:
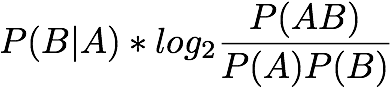
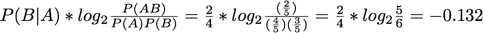
Two-Way Support:
[Yao and Zhong 1999]
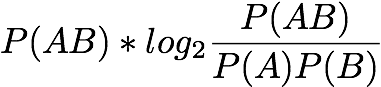
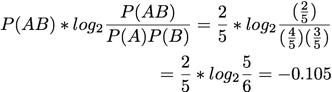
Two-Way Support Variation:
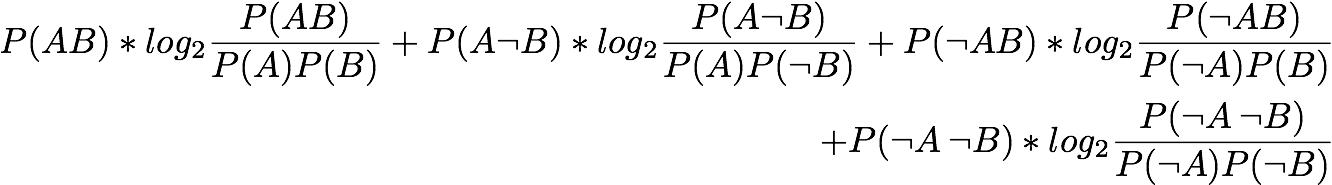
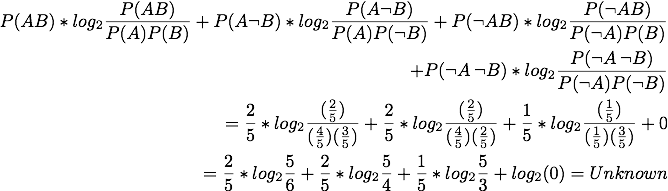
Linear Correlation Coefficient:
[Tan et al. 2002]
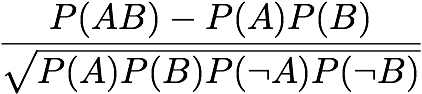
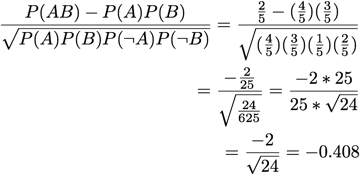
Piatetsky-Shapiro:
[Piatetsky-Shapiro 1991]
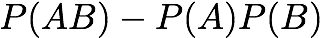
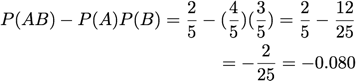
Cosine:
[Tan & Kumar 2000]
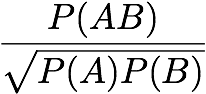
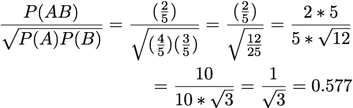
Loevinger:
[Loevinger, 1947]
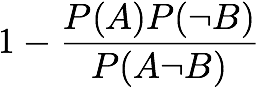
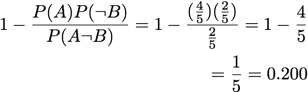
Information Gain:
[Church & Hanks 1990]
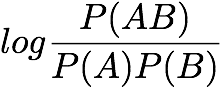
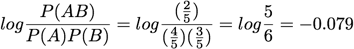
Sebag-Schoenauer:
[Sebag & Schoenauer, 1991]
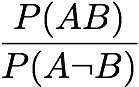
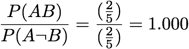
Least Contradiction:
[Aze & Kondratoff 2002]
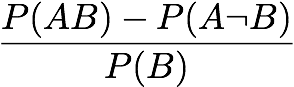
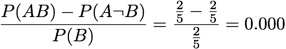
Odd Multiplier:
[Gras et al. 2001]
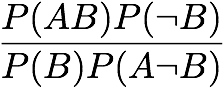
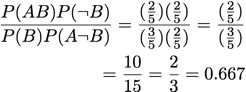
Example and Counterexample Rate:
[Vaillant et al.]
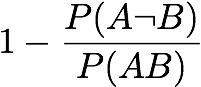
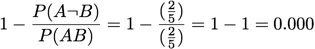
Zhang:
[Zhang 2000]
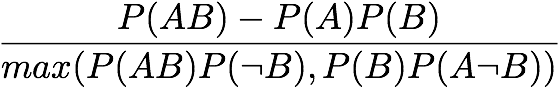
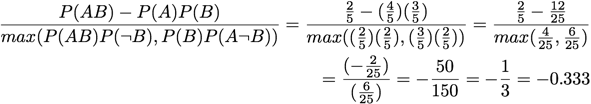
Downloadable content:
- Interestingness Measures Images (zipped .png format)
- Interestingness Measures Latex Files (zipped .ltx format)
- Example Calculation Images (zipped .png format)
- Example Calculation Latex Files (zipped .ltx format)


