Reference:

Introduction

An Iceberg-Cube contains only those cells of the data cube that meet an aggregate condition. It is called an Iceberg-Cube because it contains only some of the cells of the full cube, like the tip of an iceberg. The aggregate condition could be, for example, minimum support or a lower bound on average, min or max. The purpose of the Iceberg-Cube is to identify and compute only those values that will most likely be required for decision support queries. The aggregate condition specifies which cube values are more meaningful and should therefore be stored. This is one solution to the problem of computing versus storing data cubes.

For a three dimensional data cube, with attributes A, B and C, the Iceberg-Cube problem may be represented as:

SELECT
FROM
CUBE BY
HAVING
A,B,C, Count(*),SUM(X)
TableName
A,B,C
COUNT(*)>=minsup

where minsup is the minimum support. Minimum support is the minimum number of tuples in which a combination of attribute values must appear to be considered frequent. It is expressed as a percentage of the total number of tuples in the input table.

When an Iceberg-Cube is constructed, it may also include those totals from the original cube that satisfy the minimum support requirement. The inclusion of totals makes Iceberg-Cubes more useful for extracting previously unknown relationships from a database.

For example, suppose minimum support is 25% and we want to create an Iceberg-Cube using Table 2 as input. For a combination of attribute values to appear in the Iceberg-Cube, it must be present in at least 25% of tuples in the input table, or 2 tuples. The resulting Iceberg-Cube is shown in Table 3. Those cells in the full cube whose counts are less than 2, such as ({P1, Vancouver, Vance},1), are not present in the Iceberg-Cube.

Part StoreLocation Customer
P1 Vancouver Vance
P1 Calgary Bob
P1 Toronto Richard
P2 Toronto Allison
P2 Toronto Allison
P2 Toronto Tom
P2 Ottawa Allison
P3 Montreal Anne
Table 2: Sample Database Table
Combination Count
{P1, ANY, ANY} 3
{P2, ANY, ANY} 4
{ANY, Toronto, ANY} 4
{ANY, ANY, Allison} 3
{P2, Toronto, ANY} 3
{P2, ANY, Allison} 3
{ANY, Toronto, Allison} 2
{P2, Toronto, Allison} 2
Table 3: Sample Iceberg-Cube with Minimum Support of at least 25%

Methods for Computing Iceberg-Cubes

1. APRIORI

The APRIORI algorithm uses candidate combinations to avoid counting every possible combination of attribute values. For a combination of attribute values to satisfy the minimum support requirement, all subsets of that combination must also satisfy minimum support. The candidate combinations are found by combining only the frequent attribute value combinations that are already known. All other possible combinations are automatically eliminated because not all of their subsets would satisfy the minimum support requirement.

To do this, the algorithm first counts all single values on one pass of the data, then counts all candidate combinations of the frequent single values to identify frequent pairs. On the third pass over the data, it counts candidate combinations based on the frequent pairs to determine frequent 3-sets, and so on. This method guarantees that all frequent combinations of k values will be found in k passes over the database.

Example: Suppose the input table is as shown in Table 4. On the first pass over the data, the APRIORI algorithm determines that the single values shown in Table 5 are frequent. These single values are implicit representations of ordered sets in the ordered set representation of an Iceberg-Cube. For example, {a1} represents the combination {a1,ANY,ANY,ANY}. The candidate combinations that can be derived from these values are shown in Table 6. These combinations are counted on the second pass and the algorithm determines which of them are frequent. The result is shown in Table 7. From the frequent pairs, only one 3-set candidate combination can be derived, as shown in Table 8, and the algorithm counts this combination on the third pass over the data. The result of the third pass over the data is shown in Table 9. Since {a2, c2, d2} is not frequent no more candidate combinations can be derived, and the algorithm finishes execution.
A B C D
a1 b1 c3 d1
a1 b5 c1 d2
a1 b2 c5 d2
a2 b2 c2 d2
a2 b2 c2 d4
a2 b2 c4 d2
a2 b3 c2 d3
a3 b4 c6 d2

Table 4: Sample Input Table

Combination Count
{a1} 3
{a2} 4
{b2} 4
{c2} 3
{d2} 5
Table 5: Combinations added after first pass.
Combination
{a1,b2}
{a1,c2}
{a1,d2}
{a2, b2}
{a2,c2}
{a2,d2}
{b2,c2}
{b2,d2}
{c2,d2}
Table 6: Candidate combinations after first pass.
Combination Count
{a1,d2} 2
{a2,b2} 3
{a2,c2} 3
{b2,c2} 2
{a2,d2} 2
{b2,d2} 3
Table 7: Combinations added after second pass.
Combination
{a2,b2,c2}
{a2,b2,d2}
Table 8: Candidate combinations after second pass.
Combination Count
{a2,b2,c2} 2
{a2,b2,d2} 2
Table 9: Combinations added after third pass.

2. Top-Down Computation

Top-down computation (tdC) computes an Iceberg-Cube by traversing down a multi-dimensional lattice formed from the attributes in an input table. The lattice represents all combinations of input attributes and the relationships between those combinations. Figure 10 shows a 4-Dimensional lattice of this type. The processing path of tdC is shown in Figure 11. The algorithm begins by computing the frequent attribute value combinations for the attribute set at the top of the tree, in this case ABCD. On the same pass over the data, tdC counts value combinations for ABCD, ABC, AB and A, adding the frequent ones to the Iceberg-Cube. This is facilitated by first ordering the database by the current attribute combination, ABCD. tdC then continues to the next leaf node in the tree, ABD, and counts those attribute value combinations. For n attributes, there are 2n-1 possible combinations of those attributes, which are represented as the leaf nodes in the tree. If no pruning occurs, then tdC examines every leaf node, making 2n-1 passes over the data. Pruning can occur when no attribute value combinations are found to be frequent for a certain combination of attributes. For example, if after the combination ABCD is processed, and there are no attribute value combinations of AB that are frequent, then tdC can prune the ABD node from the processing tree because all combinations that would be counted would start with AB, except for the single attribute A, which has already been counted.

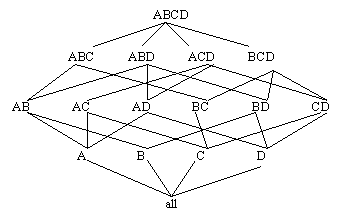
lattice
Figure 10: 4-Dimensional Lattice

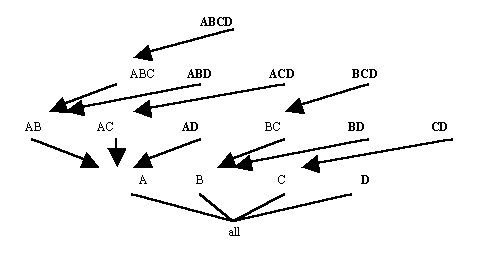
tdCTree
Figure 11: Processing Tree of tdC for Four Attributes

Example: Suppose the input to tdC is as shown in Table 4 and minimum support is 25% or 2 tuples. tdC first orders the database by ABCD, resulting in Table 10. After counting all combinations for ABCD, ABC, AB and A, the Iceberg-Cube is as shown in Table 11. tdC then orders the database by ABD, as shown in Table 12, and counts the combinations ABD, AB and A. The result is shown in Table 13. tdC continues with leaf nodes ACD, AD, BCD, BD, CD and D. No pruning occurs for this input table. The final result is shown in Table 14.
A B C D
a1 b1 c3 d1
a1 b2 c5 d2
a1 b5 c1 d2
a2 b2 c2 d2
a2 b2 c2 d4
a2 b2 c4 d2
a2 b3 c2 d3
a3 b4 c6 d2
Table 10: After Ordering by ABCD
Combination Count
{a1} 3
{a2,b2,c2} 2
{a2,b2} 3
{a2} 4
Table 11: Iceberg-Cube after ABCD
A B D
a1 b1 d1
a1 b2 d2
a1 b5 d2
a2 b2 d2
a2 b2 d2
a2 b2 d4
a2 b3 d3
a3 b4 d2
Table 12: After Ordering by ABD
Combination Count
{a1} 3
{a2,b2,d2} 2
{a2,b2} 3
{a2} 4
Table 13: Iceberg-Cube after ABD
Combination Count
{a1} 3
{a2} 4
{a2,b2} 3
{a2,b2,c2} 2
{a2,b2,d2} 2
{a2,c2} 3
{a1,d2} 2
{a2,d2} 2
{b2,c2} 2
{b2} 4
{b2,d2} 3
{c2} 3
{d2} 5
Table 14: Iceberg-Cube

The cardinality of an attribute is the number of distinct values that attribute has. The tdC algorithm prunes most efficiently when the input attributes are ordered from highest to lowest cardinality because it is more likely to prune the first attribute in that case.

3. Bottom-Up Computation

The bottom-up computation algorithm(BUC) repeatedly sorts the database as necessary to allow convenient partitioning and counting of the combinations without large main memory requirements. BUC begins by counting the frequency of the first attribute in the input table. The algorithm then partitions the database based on the frequent values of the first attribute, so that only those tuples that contain a frequent value for the first attribute are further examined. BUC then counts combinations of values for the first two attributes and again partitions the databse so only those tuples that contain frequent combinations of the first two attributes are further examined, and so on.

For a database with four attributes, A, B, C and D, the processing tree of the BUC algorithm is shown in Figure 12. As with the tdC processing tree, this is based on the 4-dimensional lattice from Figure 10. The algorithm examines attribute A, then partitions the database by the frequent values of A, sorting each partition by the next attribute, B, for ease of counting AB combinations. Within each partition, BUC counts combinations of attributes A and B. Again, once the frequent combinations are found, the database is partitioned, this time on frequent combinations of AB, and is sorted by attribute C. When no frequent combinations are found, the algorithm traverses back down the tree and ascends to the next node. For example, if there are no frequent combinations of AC, then BUC will examine combinations of AD next. In this way, BUC prunes passes over the data. As with the tdC algorithm, BUC prunes most efficiently when the attributes are ordered from highest to lowest cardinality.

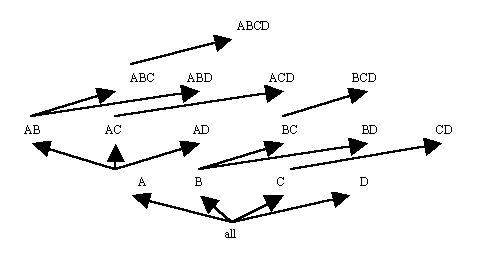
BUCTree
Figure 12: Processing Tree of BUC for Four Attributes

Example: Suppose the input table is as shown in Table 4 and minimum support is 25% or 2 tuples. BUC first counts A, finding the values a1 and a2 to be frequent. The ordered sets {a1, ANY, ANY, ANY} and {a2, ANY, ANY, ANY}, implicitly represented as simply {a1} and {a2}, and their frequencies are inserted into the Iceberg-Cube. BUC then partitions the database on the values a1 and a2 and sorts those partitions by attribute B. At AB, no value of B is frequent with a1. Then the a1 partition is sorted by C, but no value of C is frequent with a1. Only the combination {a1,d2} is inserted into the Iceberg-Cube after fully examining the a1 partition. BUC then examines the a2 partition, which is shown in Table 15. The combination {a2,b2} is found to be frequent and is inserted into the Iceberg- Cube. BUC then further partitions the frequent combination {a2,b2}. The new partition, as shown in Table 16, is sorted by attribute C. After counting all combinations of a2, b2 and any value for C, BUC inserts {a2,b2,c2} into the Iceberg-Cube, then creates partitions based on that combination of values. The new partitions, shown in Table 17, are sorted by attribute D. No combinations that include D are found to be frequent, so the algorithm descends the processing tree back to AB and then continues looking for combinations of ABD that include {a2,b2}. After sorting by attribute D, the partition shown in Table 18 results. Since the combination {a2,b2,d2} is frequent, it is inserted in the Iceberg-cube. No other values of D are frequent with {a2,b2}. The algorithm descends the processing tree to AB again. It continues looking for other frequent combinations of AB after {a2,b2}, but there are none, so eventually it returns to A. From A, processing continues at AC, looking for values of C that occur frequently with {a2}. The combination {a2,c2} occurs frequently, so processing ascends the tree to ACD, to look for values of D that occur frequently with {a2,c2}, but none are found. The algorithm returns to AC and then to A. From A processing continues at AD, where {a2,d2} is found to be frequent. Next the data is resorted based on the single attribute B, then combinations of attribute B and C, and so on. The final Iceberg-Cube is the same as for tdC, shown in Table 14.
A B C D
a2 b2 c2 d2
a2 b2 c2 d4
a2 b2 c4 d2
a2 b3 c2 d3
Table 15: Partition of {a2} on B
A B C D
a2 b2 c2 d2
a2 b2 c2 d4
a2 b2 c4 d2
Table 16: Partition of {a2,b2} on C
A B C D
a2 b2 c2 d2
a2 b2 c2 d4
Table 17: Partition of {a2,b2,c2} on D
A B D
a2 b2 d2
a2 b2 d2
a2 b2 d4

Table 18: Partition of {a2,b2} on D

4. Other Methods

For some databases the number of candidate combinations required to fit in main memory by the APRIORI algorithm becomes too large. Apart from tdC and BUC, other new methods have attempted to solve this problem. Three of these are FP-Growth, Top-k BUC and H-Mine.

FP-growth attempts to avoid candidate generation and minimize main memory use by compressing the database into a specialized data structure called an FP-tree. Unfortunately, the recursively generated conditional databases created by FP-growth may still exceed main memory size for large databases.

Top-k BUC is a specialized form of BUC, used for finding combinations with average values exceeding a specified minimum average. The average is calculated based on the sum of the values for a related measure attribute divided by the count of values. Top-k BUC also uses an H-tree (hyper-tree) for this problem.

Another recent algorithm is the H-Mine algorithm, based on partitioning the database. This algorithm requires less main memory than APRIORI and FP-Growth but more than BUC.