References:
- T. Mitchell, 1997.
- R. Myers, R. Walpole, "Tests of Hypotheses", in R. Myers, R. Walpole, Probability and Statistics for Engineers and Scientists, Second Edition, Macmillan Publishing Co., Inc., New York, NY, 1978, pp. 268 - 273.
- P. Winston, 1992.
Rule Generation
Once a decision tree has been constructed, it is a simple matter to convert it into an equivalent set of rules.
Converting a decision tree to rules before pruning has three main advantages:
- "Converting to rules allows distinguishing among the different contexts in
which a decision node is used" (Mitchell, 1997, p.72).
- Each distinct path through the tree produces a distinct rule.
- Therefore, a single path can be pruned, rather than an entire decision node.
- If the tree itself were pruned, the only possible actions would be to remove an entire node, or leave it in its original form.
- Unlike the tree, the rules do not maintain a distinction between attribute
tests that occur near the root of the tree and those that occur near the leaves.
- This allows pruning to occur without having to consider how to re-build the tree if root nodes are removed.
- Rules are easier for people to read and understand.
To generate rules, trace each path in the decision tree from root node to leaf node. Record the test outcomes as antecedents and the leaf-node classification as the consequent.
Rule Simplification Overview
Once a rule set has been devised:
- Eliminate unecessary rule antecedents to simplify the rules.
- Construct contingency tables for each rule consisting of more than one antecedent.
- Rules with only one antecedent cannot be further simplified, so we only consider those with two or more.
- To simplify a rule, eliminate antecedents that have no effect on the conclusion reached by the rule.
- A conclusion's independence from an antecendent is verified using a test for independency, which is
- a chi-square test if the expected cell frequencies are greater than 10.
- Yates' Correction for Continuity when the expected frequencies are between 5 and 10.
- Fisher's Exact Test for expected frequencies less than 5.
- Construct contingency tables for each rule consisting of more than one antecedent.
- Eliminate unecessary rules to simplify the rule set.
- Once individual rules have been simplified by eliminating redundant antecedents, simplify the entire set by eliminating unecessary rules.
- Attempt to replace those rules that share the most common consequent by a default rule that is triggered when no other rule is triggered.
- In the event of a tie, use some heuristic tie breaker to choose a default rule.
The following is a contingency table, a tabular representation of a rule.
| C1 | C2 | Marginal Sums | |
| R1 | x11 | x12 | R1T = x11 + x12 |
| R2 | x21 | x22 | R2T = x21 + x22 |
| Marginal Sums | CT1 = x11 + x21 | CT2 = x12 + x22 | T = x11 + x12 + x21 + x22 |
R1 and R2 represent the Boolean states of an antecedent for the conclusions C1 and C2
(C2 is the negation of C1).
x11, x12, x21 and x22 represent the frequencies of each antecedent-consequent pair.
R1T, R2T, CT1, CT2 are the marginal sums of the rows and columns, respectively.
The marginal sums and T, the total frequency of the table, are used to calculate expected cell values in step 3 of the test for independence.
Given a contingency table of dimensions r by c (rows x columns):
Calculate and fix the sizes of the marginal sums.
Calculate the total frequency, T, using the marginal sums.
-
Calculate the expected frequencies for each cell.
The general formula for obtaining the expected frequency of any cell xij, 1
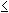 i
i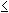 r, 1
r, 1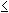 j
j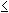 c in a contingency table is given by:
c in a contingency table is given by: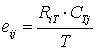
where RiT and CTj are the row total for ith row and the column total for jth column.
Select the test to be used to calculate
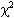 based on the highest expected frequency, m:
based on the highest expected frequency, m:if then use m 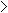 10
10Chi-Square Test 5 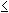 m
m 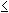 10
10Yates' Correction for Continuity m 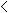 5
5Fisher's Exact Test Calculate
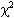 using the chosen test.
using the chosen test.-
Calculate the degrees of freedom.
df = (r - 1)(c - 1)
- Use a chi-square table with
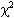 and df to determine if the conclusions are independent from the antecedent at the selected level of significance,
and df to determine if the conclusions are independent from the antecedent at the selected level of significance, 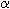 .
.
Assume
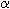 = 0.05 unless otherwise stated.
= 0.05 unless otherwise stated.- If
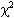
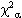
- Reject the null hypothesis of independence and accept the alternate hypothesis of dependence.
- We keep the antecedents because the conclusions are dependent upon them.
- Reject the null hypothesis of independence and accept the alternate hypothesis of dependence.
- If
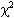
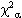
- Accept the null hypothesis of independence.
- We discard the antecedents because the conclusions are independent from them.
- Accept the null hypothesis of independence.
Chi-Square Formulae
-

Yates' Correction for Continuity
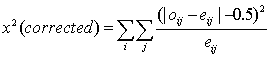
-
See Winston, pp. 437-442 for an explanation of Fisher's exact test.
Click here for an exercise in decision tree pruning.
Decision Lists
A decision list is a set of if-then statements.
It is searched sequentially for an appropriate if-then statement to be used as a rule.


