References:
- T. Mitchell, 1997.
- P. Winston, "Learning by Managing Multiple Models", in P. Winston, Artificial Intelligence, Addison-Wesley Publishing Company, 1992, pp. 411-422.
A version space is a hierarchial representation of knowledge that enables you to keep track of all the useful information supplied by a sequence of learning examples without remembering any of the examples.
The version space method is a concept learning process accomplished by managing multiple models within a version space.
Version Space Characteristics
Tentative heuristics are represented using version spaces.
A version space represents all the alternative plausible descriptions of a heuristic.
A plausible description is one that is applicable to all known positive examples and no known negative example.
A version space description consists of two complementary trees:
- One that contains nodes connected to overly general models, and
- One that contains nodes connected to overly specific models.
Node values/attributes are discrete.
Fundamental Assumptions
- The data is correct; there are no erroneous instances.
- A correct description is a conjunction of some of the attributes with values.
Diagrammatical Guidelines
There is a generalization tree and a specialization tree.
Each node is connected to a model.
Nodes in the generalization tree are connected to a model that matches everything in its subtree.
Nodes in the specialization tree are connected to a model that matches only one thing in its subtree.
Links between nodes and their models denote
- generalization relations in a generalization tree, and
- specialization relations in a specialization tree.
Diagram of a Version Space
In the diagram below, the specialization tree is colored red, and the generalization tree is colored green.
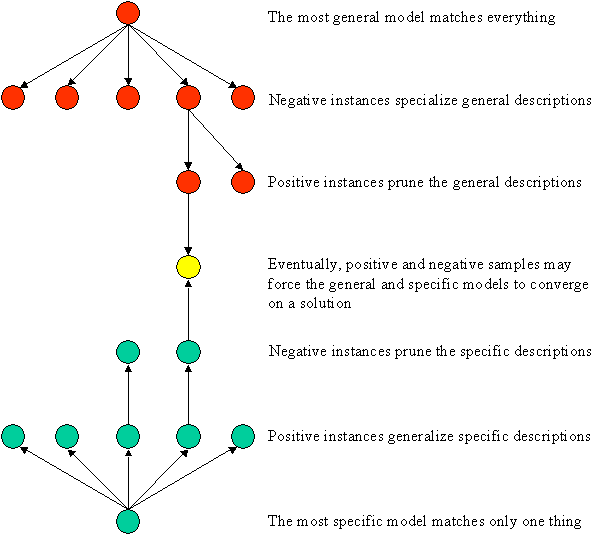
Generalization and Specialization Leads to Version Space Convergence
The key idea in version space learning is that specialization of the general models and generalization of the specific models may ultimately lead to just one correct model that matches all observed positive examples and does not match any negative examples.
That is, each time a negative example is used to specialilize the general models, those specific models that match the negative example are eliminated and each time a positive example is used to generalize the specific models, those general models that fail to match the positive example are eliminated. Eventually, the positive and negative examples may be such that only one general model and one identical specific model survive.
Version Space Method Learning Algorithm: Candidate-Elimination
The version space method handles positive and negative examples symmetrically.
Given:
- A representation language.
- A set of positive and negative examples expressed in that language.
Compute: a concept description that is consistent with all the positive examples and none of the negative examples.
Method:
- Initialize G, the set of maximally general hypotheses, to contain one element: the null description (all features are variables).
- Initialize S, the set of maximally specific hypotheses, to contain one element: the first positive example.
- Accept a new training example.
- If the example is positive:
- Generalize all the specific models to match the positive example, but ensure the following:
- The new specific models involve minimal changes.
- Each new specific model is a specialization of some general model.
- No new specific model is a generalization of some other specific model.
- Prune away all the general models that fail to match the positive example.
- Generalize all the specific models to match the positive example, but ensure the following:
- If the example is negative:
- Specialize all general models to prevent match with the negative example, but ensure the following:
- The new general models involve minimal changes.
- Each new general model is a generalization of some specific model.
- No new general model is a specialization of some other general model.
- Prune away all the specific models that match the negative example.
- Specialize all general models to prevent match with the negative example, but ensure the following:
- If S and G are both singleton sets, then:
- if they are identical, output their value and halt.
- if they are different, the training cases were inconsistent. Output this result and halt.
- else continue accepting new training examples.
- If the example is positive:
The algorithm stops when:
- It runs out of data.
- The number of hypotheses remaining is:
- 0 - no consistent description for the data in the language.
- 1 - answer (version space converges).
- 2+ - all descriptions in the language are implicitly included.
Comments on the Version Space Method
The version space method is still a trial and error method.
The program does not base its choice of examples, or its learned heuristics, on an analysis of what works or why it works, but rather on the simple assumption that what works will probably work again.
Unlike the decision tree ID3 algorithm,
- Candidate-elimination searches an incomplete set of hypotheses (ie. only a subset of the potentially teachable concepts are included in the hypothesis space).
- Candidate-elimination finds every hypothesis that is consistent with the training data, meaning it searches the hypothesis space completely.
- Candidate-elimination's inductive bias is a consequence of how well it can represent the subset of possible hypotheses it will search. In other words, the bias is a product of its search space.
- No additional bias is introduced through Candidate-eliminations's search strategy.
Advantages of the version space method:
- Can describe all the possible hypotheses in the language consistent with the data.
- Fast (close to linear).
Disadvantages of the version space method:
- Inconsistent data (noise) may cause the target concept to be pruned.
- Learning disjunctive concepts is challenging.
Click on the links below for version space method exercises:


